2次方程式
Point1 基礎事項
ax2+bx+c=0の解法
①因数分解の利用
ax2+bx+c=(px+q)(rx+s) (pr≠0)のとき
ax2+bx+c=0の解は x=-q/p, -s/r
② a=1のときb2/4-c≧0ならば、x2+bx+c=0の解は x=-b/2±√(b2/4-c)
③2次方程式の解の利用
b2-4ac≧0のとき、ax2+bx+c=0の解は
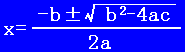
特に、bが偶数である場合、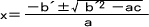
2次方程式ax2+bx+c=0の実数解の個数とD=b2-4acの符号の関係
2次方程式
ax2+bx+c=0
において、
D=b2-4ac
を、判別式(Discriminant)という。この方程式は
(1)D>0 ならば、異なる2つの実数解をもつ。
(2)D=0 ならば、重解をもつ。
(3)D<0 ならば、異なる2つの虚数解をもつ。
(1)と(2)を合わせると、この方程式は、
D≧0 ならば、実数解をもつ
Point2例題
次の2次方程式を解け。
(1) √2x2-5x+2√2=0
(2) x4-3x2-4=0
(3) 15x2-2x-1=0の2つの解の逆数が、2次方程式x2+1x+b=0の解であるように定数a,bの値を定めよ。
(4) 縦が横より5cm長い長方形がある。この長方形の縦の長さを3cm短くして横の長さを2倍にすると、面積は20cm2増加する。このとき、もとの長方形の縦の長さを求めよ。
(5) 2次方程式x2+2(2-m)x+=0について、
(ア) m=-1, m=5のときの実数の解の個数をそれぞれ求めよ。
(イ) 重解をもつようにmの値を定め、そのときの重解を求めよ。
Point3 解答
(1) x=2√2, √2/2
(2) x=±2
(3) a=2, b=-15
(4) もとの長方形の長さをxとすると、もとの長方形の面積は x(x-5)cm2
この長方形の縦の長さを3cm短くして、横の長さを2倍にした長方形の面積は
(x-3)×2(x-5)xm2
よって、条件から 2(x-3)(x-5)-x(x-5)=20 これを解くと x=1, 10
x>5であるから x=10 よって、縦の長さは10cm
(5) D'=(2-m)2-1・m=m2-5m+4
(ア) m=-1のとき個数は2個 m=5のとき個数は2個
(イ) 与式が重解をもつとき D’=(m-1)(m-4)=0
よって m=1, 4
m=1のとき重解はx=-{2(2-m)}/2=-1
m=4のとき重解はx=m-2=2
したがって m=1のときx=-1;m=4のときx=2
ax2+bx+c=0の解法
①因数分解の利用
ax2+bx+c=(px+q)(rx+s) (pr≠0)のとき
ax2+bx+c=0の解は x=-q/p, -s/r
② a=1のときb2/4-c≧0ならば、x2+bx+c=0の解は x=-b/2±√(b2/4-c)
③2次方程式の解の利用
b2-4ac≧0のとき、ax2+bx+c=0の解は
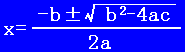
特に、bが偶数である場合、
2次方程式ax2+bx+c=0の実数解の個数とD=b2-4acの符号の関係
2次方程式
ax2+bx+c=0
において、
D=b2-4ac
を、判別式(Discriminant)という。この方程式は
(1)D>0 ならば、異なる2つの実数解をもつ。
(2)D=0 ならば、重解をもつ。
(3)D<0 ならば、異なる2つの虚数解をもつ。
(1)と(2)を合わせると、この方程式は、
D≧0 ならば、実数解をもつ
Point2
次の2次方程式を解け。
(1) √2x2-5x+2√2=0
(2) x4-3x2-4=0
(3) 15x2-2x-1=0の2つの解の逆数が、2次方程式x2+1x+b=0の解であるように定数a,bの値を定めよ。
(4) 縦が横より5cm長い長方形がある。この長方形の縦の長さを3cm短くして横の長さを2倍にすると、面積は20cm2増加する。このとき、もとの長方形の縦の長さを求めよ。
(5) 2次方程式x2+2(2-m)x+=0について、
(ア) m=-1, m=5のときの実数の解の個数をそれぞれ求めよ。
(イ) 重解をもつようにmの値を定め、そのときの重解を求めよ。
Point3
(1) x=2√2, √2/2
(2) x=±2
(3) a=2, b=-15
(4) もとの長方形の長さをxとすると、もとの長方形の面積は x(x-5)cm2
この長方形の縦の長さを3cm短くして、横の長さを2倍にした長方形の面積は
(x-3)×2(x-5)xm2
よって、条件から 2(x-3)(x-5)-x(x-5)=20 これを解くと x=1, 10
x>5であるから x=10 よって、縦の長さは10cm
(5) D'=(2-m)2-1・m=m2-5m+4
(ア) m=-1のとき個数は2個 m=5のとき個数は2個
(イ) 与式が重解をもつとき D’=(m-1)(m-4)=0
よって m=1, 4
m=1のとき重解はx=-{2(2-m)}/2=-1
m=4のとき重解はx=m-2=2
したがって m=1のときx=-1;m=4のときx=2
br→
main_box