俀師娭悢偺嵟戝偲嵟彫
Point1丂婎慴帠崁
俀師娭悢偺嵟戝偲嵟彫
婎杮宍丂倷亖a(x亅p)2亄q
丂丂丂丂丂a>0偺偲偒丂倶亖倫偱嵟彫抣倯丂嵟戝抣偼側偄
丂丂丂丂丂a<0偺偲偒丂倶亖倫偱嵟戝抣倯丂嵟彫抣偼側偄
堦斒宍丂倷亖ax2亄bx亄c
丂丂丂丂丂暯曽姰惉偟偰婎杮宍偵捈偡丅
嬫娫倛亝倶亝倠偵偍偗傞俀師娭悢偺嵟戝丒嵟彫
俀師娭悢偺丄嬫娫倛亝倶亝倠偵偍偗傞嵟戝偲嵟彫偼丄捀揰偺倶嵗昗倫偺埵抲偵傛傝丄師偺応崌偵暘偐傟傞乮忋偵撌偺僌儔僼側傜嵟戝偲嵟彫偑擖傟懼傢傞乯丅
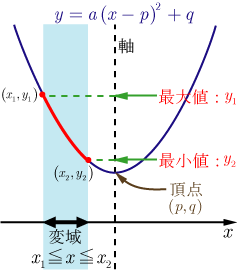 丂倫偑嬫娫偺塃奜
丂倫偑嬫娫偺塃奜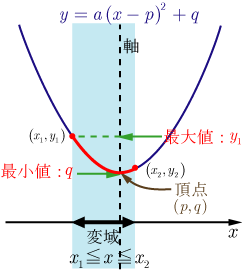 丂塃敿暘
丂塃敿暘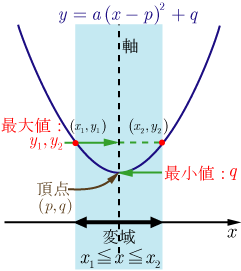 丂拞墰
丂拞墰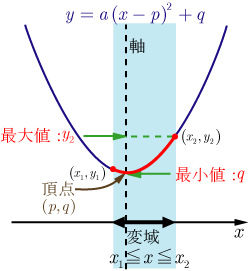 丂嵍敿暘
丂嵍敿暘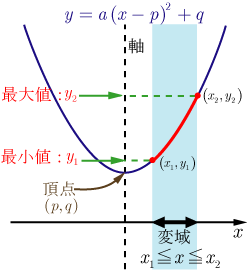 丂嵍奜
丂嵍奜
Point2丂椺戣
侾丏丂師偺娭悢偺嵟戝抣偲嵟彫抣傪媮傔傛丅
乮侾乯丂倷亖俀倶2亄俁倶亄侾丂乮亅1/2亝倶<1/2乯丂丂丂乮俀乯丂倷亖亅1/2倶2亄俀倶亄3/2丂乮1亝倶亝5乯
乮俁乯丂倷亖倶2亄ax亄b丂乮亅1亝倶亝2乯
俀丏丂娭悢倷亖亅倶2亄俀倢倠亅倢2亅俀倢亅侾乮亅侾亝倶亝侽乯偺嵟戝抣偑侽偵側傞傛偆側掕悢倢偺抣傪媮傔傛丅
俁丏丂俀師娭悢倷亖亅俀倶2亄俇倶亄侾偺a亝倶亝a亄侾偵偍偗傞嵟彫抣傪媮傔傛丅
Point3丂夝摎
侾丏丂乮侾乯丂倶亖亅1/2偱嵟彫抣侽丄嵟戝抣側偟丂丂丂乮俀乯丂倶亖俀偱嵟戝抣7/2丄嵟彫抣亅侾
丂乮俁乯丂嵟戝抣偼a<亅侾偺偲偒丂倶亖亅侾偱亅a亄倐亄侾丄亅侾亝a偺偲偒倶亖俀偱俀a亄倐亄係
丂丂丂丂 嵟彫抣偼a<亅係偺偲偒倶亖俀偱俀a亄倐亄係丄亅係亝a<2偺偲偒倶亖亅a/2偱亅a2/4亄倐
丂丂丂丂丂丂丂丂丂丂俀亝a偺偲偒倶亖亅侾偱亅a亄倐亄侾
俀丏丂倷亖亅乮倶亅倢乯2亅俀倢亅侾乧嘆
丂[侾]丂倢亙亅侾偺偲偒
丂丂丂倶亖亅侾偱嵟戝抣亅乮倢2亄係倢亄俀乯傪偲傞丅亪倢亖亅俀亅併俀
丂[俀]丂亅侾亝倢亝侽偺偲偒
丂丂丂嵟戝抣偼亅俀倢亅侾偱偁傞偐傜丄亅俀倢亅侾亖侽偲偍偔偲倢亖亅1/2丂偙傟偼亅侾亝倢亝侽傪枮偨偡丅
丂[俁]丂侽亙倢偺偲偒
丂丂丂倶亖侽偱嵟戝抣亅乮倢2亄俀倢亄侾乯傪偲傞丅亪倢亖亅侾偲側傝丄偙傟偼倢亜侽偵斀偡傞偐傜晄揔丅
丂埲忋偵傛傝丄媮傔傞倢偺抣偼丂亅俀亅併俀丄亅1/2
俁丏丂倷亖亅俀乮倶亅3/2乯2亄11/2
丂偙偙偱丄倖乮a乯亖亅俀a2亄俇a亄侾丄倖乮a亄侾乯亖亅俀a2亄俀a亄俆偱偁傝丄倖乮a乯亖倖乮a亄侾乯偲偡傞偲
丂a亖侾丂丂丂傛偭偰丄
丂a<1偺偲偒倶亖a偱嵟彫抣亅俀a2亄俇a亄侾
丂侾亝a偺偲偒倶亖a亄侾偱嵟彫抣亅俀a2亄俀a亄俆傪偲傞丅
俀師娭悢偺嵟戝偲嵟彫
婎杮宍丂倷亖a(x亅p)2亄q
丂丂丂丂丂a>0偺偲偒丂倶亖倫偱嵟彫抣倯丂嵟戝抣偼側偄
丂丂丂丂丂a<0偺偲偒丂倶亖倫偱嵟戝抣倯丂嵟彫抣偼側偄
堦斒宍丂倷亖ax2亄bx亄c
丂丂丂丂丂暯曽姰惉偟偰婎杮宍偵捈偡丅
嬫娫倛亝倶亝倠偵偍偗傞俀師娭悢偺嵟戝丒嵟彫
俀師娭悢偺丄嬫娫倛亝倶亝倠偵偍偗傞嵟戝偲嵟彫偼丄捀揰偺倶嵗昗倫偺埵抲偵傛傝丄師偺応崌偵暘偐傟傞乮忋偵撌偺僌儔僼側傜嵟戝偲嵟彫偑擖傟懼傢傞乯丅
 丂倫偑嬫娫偺塃奜
丂倫偑嬫娫偺塃奜 丂塃敿暘
丂塃敿暘 丂拞墰
丂拞墰 丂嵍敿暘
丂嵍敿暘 丂嵍奜
丂嵍奜Point2丂
侾丏丂師偺娭悢偺嵟戝抣偲嵟彫抣傪媮傔傛丅
乮侾乯丂倷亖俀倶2亄俁倶亄侾丂乮亅1/2亝倶<1/2乯丂丂丂乮俀乯丂倷亖亅1/2倶2亄俀倶亄3/2丂乮1亝倶亝5乯
乮俁乯丂倷亖倶2亄ax亄b丂乮亅1亝倶亝2乯
俀丏丂娭悢倷亖亅倶2亄俀倢倠亅倢2亅俀倢亅侾乮亅侾亝倶亝侽乯偺嵟戝抣偑侽偵側傞傛偆側掕悢倢偺抣傪媮傔傛丅
俁丏丂俀師娭悢倷亖亅俀倶2亄俇倶亄侾偺a亝倶亝a亄侾偵偍偗傞嵟彫抣傪媮傔傛丅
Point3
侾丏丂乮侾乯丂倶亖亅1/2偱嵟彫抣侽丄嵟戝抣側偟丂丂丂乮俀乯丂倶亖俀偱嵟戝抣7/2丄嵟彫抣亅侾
丂乮俁乯丂嵟戝抣偼a<亅侾偺偲偒丂倶亖亅侾偱亅a亄倐亄侾丄亅侾亝a偺偲偒倶亖俀偱俀a亄倐亄係
丂丂丂丂 嵟彫抣偼a<亅係偺偲偒倶亖俀偱俀a亄倐亄係丄亅係亝a<2偺偲偒倶亖亅a/2偱亅a2/4亄倐
丂丂丂丂丂丂丂丂丂丂俀亝a偺偲偒倶亖亅侾偱亅a亄倐亄侾
俀丏丂倷亖亅乮倶亅倢乯2亅俀倢亅侾乧嘆
丂[侾]丂倢亙亅侾偺偲偒
丂丂丂倶亖亅侾偱嵟戝抣亅乮倢2亄係倢亄俀乯傪偲傞丅亪倢亖亅俀亅併俀
丂[俀]丂亅侾亝倢亝侽偺偲偒
丂丂丂嵟戝抣偼亅俀倢亅侾偱偁傞偐傜丄亅俀倢亅侾亖侽偲偍偔偲倢亖亅1/2丂偙傟偼亅侾亝倢亝侽傪枮偨偡丅
丂[俁]丂侽亙倢偺偲偒
丂丂丂倶亖侽偱嵟戝抣亅乮倢2亄俀倢亄侾乯傪偲傞丅亪倢亖亅侾偲側傝丄偙傟偼倢亜侽偵斀偡傞偐傜晄揔丅
丂埲忋偵傛傝丄媮傔傞倢偺抣偼丂亅俀亅併俀丄亅1/2
俁丏丂倷亖亅俀乮倶亅3/2乯2亄11/2
丂偙偙偱丄倖乮a乯亖亅俀a2亄俇a亄侾丄倖乮a亄侾乯亖亅俀a2亄俀a亄俆偱偁傝丄倖乮a乯亖倖乮a亄侾乯偲偡傞偲
丂a亖侾丂丂丂傛偭偰丄
丂a<1偺偲偒倶亖a偱嵟彫抣亅俀a2亄俇a亄侾
丂侾亝a偺偲偒倶亖a亄侾偱嵟彫抣亅俀a2亄俀a亄俆傪偲傞丅
br仺
main_box