娭悢偲僌儔僼
Point1丂婎慴帠崁
娭悢
嘆2偮偺曄悢x,y偺娫偵偁傞娭學偑偁偭偰丄x偺抣偑掕傑傞偲偦傟偵偲傕側偭偰y偺抣偑1偮偵掕傑傞偲偒丂y偼x偺娭悢偱偁傞丂偲偄偄丄婰崋偱丂y=f(x),y=g(x)丂側偳偲昞偡丅
丂傑偨丄x偺娭悢傪扨偵娭悢f(x)偲傕偄偆丅
嘇娭悢y=f(x)偵偍偄偰丄曄悢x偺抣偺偲傝偆傞斖埻丄偡側傢偪x偺曄堟傪偙偺娭悢偺丂掕丂丂媊堟丂偲偄偆丅傑偨丄x偑掕媊堟撪偺偡傋偰偺抣傪偲傞偲偒丄x偵懳墳偡傞f(x)偺抣偺偲傝丂偆傞斖埻丄偡側傢偪y偺曄堟傪偙偺娭悢偺丂抣堟丂偲偄偆丅
y=ax亄b偺僌儔僼
嘆丂a亗侽偺偲偒丂侾師娭悢y亖ax亄b偺僌儔僼
丂孹偒偑a丄y幉忋偺愗曅(y愗曅)偑b偺捈慄
丂a亜侽丂側傜丂塃忋偑傝丂丂丂a亙侽丂側傜丂塃壓偑傝
嘇丂a亖侽偺偲偒丂y亖b偺僌儔僼
丂孹偒偑侽丄y愗曅偑b偺y幉忋偵悅捈側捈慄
Point2丂椺戣
(1)丂倖(倶)亖係倶亅俁丄倗(倶)亖亅俁倶2偺偲偒丄師偺抣傪媮傔傛丅
丂f(3/2)丂丂丂f(x+2)丂丂丂g(-1+併3)丂丂丂g(a2)
(2)丂娭悢y=併3x-2(併3亝x亙2+併3)偺抣堟傪媮傔傛丅傑偨嵟戝抣丒嵟彫抣傪媮傔傛丅
(3)丂[a]偼幚悢a傪挻偊側偄嵟戝偺惍悢傪昞偡傕偺偲偡傞丅
丂娭悢y=-[x](-3亝x亝2)偺僌儔僼傪偐偗丅
(4)丂師偺娭悢偺僌儔僼傪偐偗丅傑偨丄偦偺抣堟傪偄偊丅
丂嘆丂倷亖乥倶乥亄侾(亅俁亝倶亝俀)丂丂丂嘇丂倷亖乥俀倶亄係乥(亅俁亝倶亙侾)
Point3丂夝摎
(1)丂f(x),g(x)偵倶亖乧傪戙擖丅
丂俁丂丂丂丂丂係倶亄俆丂丂丂丂丂亅侾俀亄俇併俁丂丂丂丂丂亅俁a4
(2)丂抣堟偼丂侾亝倷亙侾亄俀併俁
丂倶亖併俁偱嵟彫抣侾丄嵟戝抣偼側偟丅
(3)
丂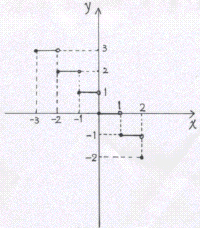
(4)丂嘆
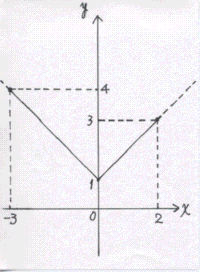 抣堟偼丂侾亝倷亝係
抣堟偼丂侾亝倷亝係
嘇
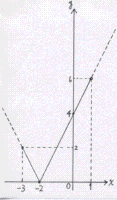 抣堟偼丂侽亝倷亙俇
抣堟偼丂侽亝倷亙俇
娭悢
嘆2偮偺曄悢x,y偺娫偵偁傞娭學偑偁偭偰丄x偺抣偑掕傑傞偲偦傟偵偲傕側偭偰y偺抣偑1偮偵掕傑傞偲偒丂y偼x偺娭悢偱偁傞丂偲偄偄丄婰崋偱丂y=f(x),y=g(x)丂側偳偲昞偡丅
丂傑偨丄x偺娭悢傪扨偵娭悢f(x)偲傕偄偆丅
嘇娭悢y=f(x)偵偍偄偰丄曄悢x偺抣偺偲傝偆傞斖埻丄偡側傢偪x偺曄堟傪偙偺娭悢偺丂掕丂丂媊堟丂偲偄偆丅傑偨丄x偑掕媊堟撪偺偡傋偰偺抣傪偲傞偲偒丄x偵懳墳偡傞f(x)偺抣偺偲傝丂偆傞斖埻丄偡側傢偪y偺曄堟傪偙偺娭悢偺丂抣堟丂偲偄偆丅
y=ax亄b偺僌儔僼
嘆丂a亗侽偺偲偒丂侾師娭悢y亖ax亄b偺僌儔僼
丂孹偒偑a丄y幉忋偺愗曅(y愗曅)偑b偺捈慄
丂a亜侽丂側傜丂塃忋偑傝丂丂丂a亙侽丂側傜丂塃壓偑傝
嘇丂a亖侽偺偲偒丂y亖b偺僌儔僼
丂孹偒偑侽丄y愗曅偑b偺y幉忋偵悅捈側捈慄
Point2丂
(1)丂倖(倶)亖係倶亅俁丄倗(倶)亖亅俁倶2偺偲偒丄師偺抣傪媮傔傛丅
丂f(3/2)丂丂丂f(x+2)丂丂丂g(-1+併3)丂丂丂g(a2)
(2)丂娭悢y=併3x-2(併3亝x亙2+併3)偺抣堟傪媮傔傛丅傑偨嵟戝抣丒嵟彫抣傪媮傔傛丅
(3)丂[a]偼幚悢a傪挻偊側偄嵟戝偺惍悢傪昞偡傕偺偲偡傞丅
丂娭悢y=-[x](-3亝x亝2)偺僌儔僼傪偐偗丅
(4)丂師偺娭悢偺僌儔僼傪偐偗丅傑偨丄偦偺抣堟傪偄偊丅
丂嘆丂倷亖乥倶乥亄侾(亅俁亝倶亝俀)丂丂丂嘇丂倷亖乥俀倶亄係乥(亅俁亝倶亙侾)
Point3
(1)丂f(x),g(x)偵倶亖乧傪戙擖丅
丂俁丂丂丂丂丂係倶亄俆丂丂丂丂丂亅侾俀亄俇併俁丂丂丂丂丂亅俁a4
(2)丂抣堟偼丂侾亝倷亙侾亄俀併俁
丂倶亖併俁偱嵟彫抣侾丄嵟戝抣偼側偟丅
(3)
丂

(4)丂嘆
 抣堟偼丂侾亝倷亝係
抣堟偼丂侾亝倷亝係嘇
 抣堟偼丂侽亝倷亙俇
抣堟偼丂侽亝倷亙俇br仺
main_box