旝暘學悢
Point1丂婎慴帠崁
暯嬒曄壔棪偲旝暘學悢
娭悢倖乮倶乯偵偍偄偰丄倶偺抣偑a偐傜倐傑偱曄壔偡傞偲偒丄倷偺曄壔検倖乮倐乯亅倖乮a乯偺丄倶偺曄壔検b亅a偵懳偡傞妱崌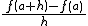 傪丄倶偑a偐傜倐傑偱曄壔偡傞偲偒偺娭悢倖乮倶乯偺丂暯嬒曄壔棪丂偲偄偆丅丂娭悢倖乮倶乯偺暯嬒曄壔棪偵偍偄偰丄a偺抣傪掕傔丄倐傪a偵尷傝側偔嬤偯偗傞偲偒丄暯嬒曄壔棪偑偁傞堦掕偺抣兛偵尷傝側偔嬤偯偔応崌丄偙偺抣兛傪丄娭悢倖乮倶乯偺倶亖a偵偍偗傞丂旝暘學悢丂傑偨偼曄壔棪偲偄偄丄丂倖乫乮a乯丂偱昞偡丅
傪丄倶偑a偐傜倐傑偱曄壔偡傞偲偒偺娭悢倖乮倶乯偺丂暯嬒曄壔棪丂偲偄偆丅丂娭悢倖乮倶乯偺暯嬒曄壔棪偵偍偄偰丄a偺抣傪掕傔丄倐傪a偵尷傝側偔嬤偯偗傞偲偒丄暯嬒曄壔棪偑偁傞堦掕偺抣兛偵尷傝側偔嬤偯偔応崌丄偙偺抣兛傪丄娭悢倖乮倶乯偺倶亖a偵偍偗傞丂旝暘學悢丂傑偨偼曄壔棪偲偄偄丄丂倖乫乮a乯丂偱昞偡丅
嘆丂嬌尷抣
丂娭悢倖乮倶乯偵偍偄偰丄倶偑a偲堎側傞抣傪偲傝側偑傜a偵尷傝側偔嬤偯偔偲偒丄倖乮倶乯偑偁傞堦掕偺抣兛偵尷傝側偔嬤偯偔応崌丄偙偺抣兛傪丄倶仺a偺偲偒偺倖乮倶乯偺丂嬌尷抣丂偲偄偆丅偙傟傪丄師偺傛偆偵昞偡丅
丂丂丂倶仺a偺偲偒丂倖乮倶乯仺兛丂傑偨偼丂lim倖乮倶乯亖兛
嘇丂旝暘學悢
丂娭悢倖乮倶乯偺倶亖a偵偍偗傞旝暘學悢偺掕媊
丂丂丂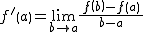 丂傑偨偼丂
丂傑偨偼丂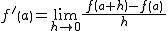
旝暘學悢偺恾宍揑堄枴
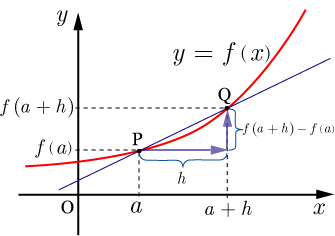
丂倶亖a偵偍偗傞娭悢倖乮倶乯偺旝暘學悢倖'(a乯偼丄嬋慄倷亖倖乮倶乯忋偺揰A乮a丆倖乮a乯乯偵偍偗傞嬋慄偺丂愙慄偺孹偒丂傪昞偡丅
Point2丂椺戣
娭悢倲亖俁倶2亅俆倶偵偮偄偰丄師偺傕偺傪媮傔傛丅
乮侾乯丂倶亖俀偐傜倶亖係傑偱曄壔偡傞偲偒偺暯嬒曄壔棪丅
乮俀乯丂倶亖俀偵偍偗傞旝暘學悢丅
乮俁乯丂曻暔慄倷亖俁倶2亅俆倶偺倶亖們偵偍偗傞愙慄偺孹偒偑乮侾乯偱媮傔偨暯嬒曄壔棪偺抣偵摍偟偄偲偒丄偦偺們偺抣丅
Point3丂夝摎
乮侾乯丂乷倖乮係乯亅倖乮俀乯乸/係亅俀亖侾俁
乮俀乯丂lim乷倖乮俀亄倛乯亅倖乮俀乯乸/h亖俈
乮俁乯丂lim乷俁乮們亄倛乯2亅俆乮們亄倛乯亅乮俁們2亅俆們乯乸/h亖俇們亅俆
丂丂丂俇們亅俆亖侾俁丂側偺偱丄丂亪們亖俁
暯嬒曄壔棪偲旝暘學悢
娭悢倖乮倶乯偵偍偄偰丄倶偺抣偑a偐傜倐傑偱曄壔偡傞偲偒丄倷偺曄壔検倖乮倐乯亅倖乮a乯偺丄倶偺曄壔検b亅a偵懳偡傞妱崌

嘆丂嬌尷抣
丂娭悢倖乮倶乯偵偍偄偰丄倶偑a偲堎側傞抣傪偲傝側偑傜a偵尷傝側偔嬤偯偔偲偒丄倖乮倶乯偑偁傞堦掕偺抣兛偵尷傝側偔嬤偯偔応崌丄偙偺抣兛傪丄倶仺a偺偲偒偺倖乮倶乯偺丂嬌尷抣丂偲偄偆丅偙傟傪丄師偺傛偆偵昞偡丅
丂丂丂倶仺a偺偲偒丂倖乮倶乯仺兛丂傑偨偼丂lim倖乮倶乯亖兛
嘇丂旝暘學悢
丂娭悢倖乮倶乯偺倶亖a偵偍偗傞旝暘學悢偺掕媊
丂丂丂
旝暘學悢偺恾宍揑堄枴
丂倶亖a偵偍偗傞娭悢倖乮倶乯偺旝暘學悢倖'(a乯偼丄嬋慄倷亖倖乮倶乯忋偺揰A乮a丆倖乮a乯乯偵偍偗傞嬋慄偺丂愙慄偺孹偒丂傪昞偡丅
Point2丂
娭悢倲亖俁倶2亅俆倶偵偮偄偰丄師偺傕偺傪媮傔傛丅
乮侾乯丂倶亖俀偐傜倶亖係傑偱曄壔偡傞偲偒偺暯嬒曄壔棪丅
乮俀乯丂倶亖俀偵偍偗傞旝暘學悢丅
乮俁乯丂曻暔慄倷亖俁倶2亅俆倶偺倶亖們偵偍偗傞愙慄偺孹偒偑乮侾乯偱媮傔偨暯嬒曄壔棪偺抣偵摍偟偄偲偒丄偦偺們偺抣丅
Point3
乮侾乯丂乷倖乮係乯亅倖乮俀乯乸/係亅俀亖侾俁
乮俀乯丂lim乷倖乮俀亄倛乯亅倖乮俀乯乸/h亖俈
乮俁乯丂lim乷俁乮們亄倛乯2亅俆乮們亄倛乯亅乮俁們2亅俆們乯乸/h亖俇們亅俆
丂丂丂俇們亅俆亖侾俁丂側偺偱丄丂亪們亖俁
br仺
main_box