Point1　基礎事項
導関数
関数ｆ（ｘ）の導関数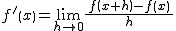　

ｙ＝ｘⁿと定数関数の導関数
関数ｙ＝ｘⁿの導関数は　ｙ’＝ｎｘ^n-1
定数関数ｙ＝Cの導関数は　Y'＝０

導関数の公式
u、ｖはｘの関数とし、ｋ、ｌは定数とする。
　　　定数倍　（ｋu）’＝ｋu’
　　　和　　　　（u＋ｖ）’＝u’＋ｖ’
　　　まとめて　（ku＋lv）’＝ku’＋lv’

Point2　例題
１．　次の関数を微分せよ。また、ｆ’（２）を求めよ。
　（ア）　ｆ（ｘ）＝４ｘ³＋２ｘ　　　　　（イ）　ｆ（ｘ）＝２ｘ³＋ｘ²－９ｘ－４
　（ウ）　ｆ（ｘ）＝（ｘ－１）（２ｘ＋３） （エ）　ｆ（ｘ）＝（－２ｘ＋１）³

２．　ｆ（ｘ）は３次の整式で、ｘ³の係数が１、ｆ（１）＝２、ｆ（－１）＝－２、ｆ’（－１）＝０である。このとき、ｆ（ｘ）を求めよ。

３．　球の半径が１ｍから毎秒１０ｃｍの割合で大きくなるとする。
　（１）　１０秒後における球の表面積の変化率を求めよ。
　（２）　球の半径が３ｍになるときの球の体積の時間に対する変化率を求めよ。

Point3　解答
１．　（ア）　ｆ’（ｘ）＝１２ｘ²＋２　　　ｆ’（２）＝５０
　　　（イ）　ｆ’（ｘ）＝６ｘ²＋２ｘ－９　　　ｆ’（２）＝１９
　　　（ウ）　ｆ’（ｘ）＝４ｘ＋１　　　ｆ’（２）＝９
　　　（エ）　ｆ’（ｘ）＝－２４ｘ²＋２４ｘ－６　　　ｆ’（２）＝－５４

２．　ｆ（ｘ）＝ｘ³＋ax²＋bx＋c　とおくと　ｆ’（ｘ）＝３ｘ²＋２ax＋b
　　　ｆ（１）＝１＋a＋ｂ＋ｃ＝２
　　　ｆ（－１）＝－１＋a－ｂ＋ｃ＝－２
　　　ｆ’（－１）＝３－２a＋ｂ＝０
　　　∴a＝２、ｂ＝１、ｃ＝－２
　　　したがって　ｆ（ｘ）＝ｘ³＋２ｘ²＋ｘ－２

３．　（１）　ｔ秒後の球の半径をｒｍ、表面積をS㎡とする。
　　　　　条件から　ｒ＝１＋０．１ｔ　∴S＝４π（１＋０．１ｔ）²…①
　　　　　①の両辺をｔで微分すると、　ｄS/ｄｔ＝４π・２・０．１（１＋０．１ｔ）…②
　　　　　ｔ＝１０とおいて　１．６π㎡/秒
　　　（２）　体積をV㎥とする。　条件からｒ＝１＋０．１ｔ　∴V＝４/３π（１＋０．１ｔ）³…①
　　　　　①の両辺をｔで微分すると、　dV/dt＝４/３π・３・０．１（１＋０．１ｔ）²…②
　　　　　１＋０．１ｔ＝３からｔ＝２０　∴ｔ＝２０とおいて　３．６π㎥/秒