関数の増減と極大・極小
Point1 基礎事項
関数の増減
ある区間で常に
f’(x)>0 ならば f(x)はその区間で単調に 増加 する。
f’(x)<0 ならば f(x)はその区間で単調に 減少 する。
f’(x)=0 ならば f(x)はその区間で 定数 である。
関数の極大・極小
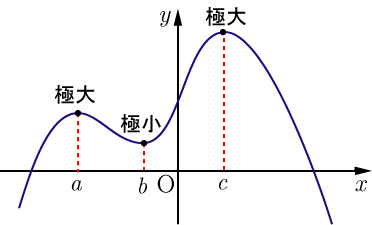
① 関数y=f(x)の極値を求めるには、f’(x)=0となるxの値を求め、その前後におけるf’(x)の符号を調べる。
② f’(x)の符号がx=aの前後で
正から負 に変わるとき、f(a)は 極大値
負から正 に変わるとき、f(a)は 極小値
極大値と極小値をまとめて 極値 という。
Point2例題
1. xについての3次関数f(x)=x3+px2+27xがある。f(x)が単調に増加する関数となるpの最大値を求めよ。
2. 次の関数の極値を求めよ。また、そのグラフをかけ。
(1) y=2x3-6x-4 (2) y=|x3-x2|
Point3 解答
1. 3次関数f(x)が単調増加関数である条件は、常にf’(x)≧0が成り立つことである。
よって、判別式Dについて D/4=p2-3・27≦0
これを解いて -9≦p≦9 よってpの最大値は9
2. (1) 増減表 x=-1のとき極大値0、x=1のとき極小値-8
(2) y’=3x2-2x=x(3x-2) x=0,2/3
増減表 x=2/3のとき極大値4/27、x=0,1のとき極小値0
関数の増減
ある区間で常に
f’(x)>0 ならば f(x)はその区間で単調に 増加 する。
f’(x)<0 ならば f(x)はその区間で単調に 減少 する。
f’(x)=0 ならば f(x)はその区間で 定数 である。
増減表とは,関数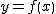 のグラフの概略を描くために,
のグラフの概略を描くために,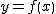 の符号を求めて関数
の符号を求めて関数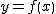 の増加および減少の様子を表にまとめたものである。
の増加および減少の様子を表にまとめたものである。
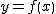 |
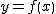 |
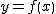 |
|||
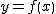 |
+ | 0 | - | 0 | + |
 |
32 | 0 |
関数の極大・極小
① 関数y=f(x)の極値を求めるには、f’(x)=0となるxの値を求め、その前後におけるf’(x)の符号を調べる。
② f’(x)の符号がx=aの前後で
正から負 に変わるとき、f(a)は 極大値
負から正 に変わるとき、f(a)は 極小値
極大値と極小値をまとめて 極値 という。

Point2
1. xについての3次関数f(x)=x3+px2+27xがある。f(x)が単調に増加する関数となるpの最大値を求めよ。
2. 次の関数の極値を求めよ。また、そのグラフをかけ。
(1) y=2x3-6x-4 (2) y=|x3-x2|
Point3
1. 3次関数f(x)が単調増加関数である条件は、常にf’(x)≧0が成り立つことである。
よって、判別式Dについて D/4=p2-3・27≦0
これを解いて -9≦p≦9 よってpの最大値は9
2. (1) 増減表 x=-1のとき極大値0、x=1のとき極小値-8
| x | ・・・ | -1 | ・・・ | 1 | ・・・ |
| y’ | + | 0 | - | 0 | + |
| y | 極大 | 極小 |
(2) y’=3x2-2x=x(3x-2) x=0,2/3
増減表 x=2/3のとき極大値4/27、x=0,1のとき極小値0
| x | ・・・ | 0 | ・・・ | 2/3 | ・・・ |
| y’ | + | 0 | - | 0 | + |
| y | 極大 | 極小 |
br→
main_box