Point1　基礎事項
三角関数のグラフ





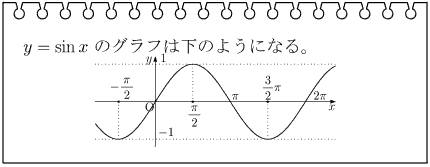
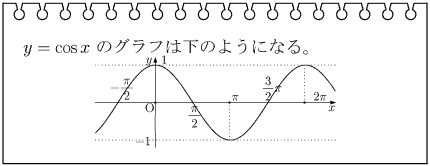
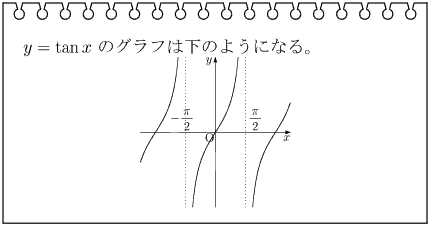
sin、cosのグラフのΘは実数全体、−１≦ｙ≦１
tanのグラフはΘ≠π/2＋ｎπ（ｎは整数）、ｙはすべての実数値をとる。直線Θ＝π/2＋ｎπ（ｎは整数）が漸近線

周期関数

いろいろな三角関数のグラフ

奇関数・偶関数

Point2　例題
次の関数のグラフを書け。また、周期を求めよ。
（１）　ｙ＝２tanΘ　　　（２）　ｙ＝cos（Θ＋π/3）　　　（３）　ｙ＝cos２Θ　　　（４）　ｙ＝−sinΘ＋１

Point3　解答
（１）　周期＝π

（２）　周期＝２π

（３）　周期＝π

（４）　周期＝２π