Point1　基礎事項
チェバの定理

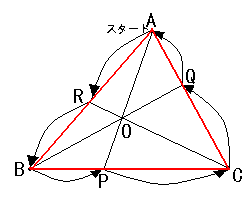
上図の△ABCの3頂点A、B、Cと三角形の辺上またはその延長と交わるとき、
交点をそれぞれP、Q、Rとすると


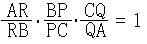
チェバの定理の逆
△ABCの辺BC、CA、ABまたはその辺の延長上に、それぞれ点P、Q、Rがあり、この3点のうちの1個または3個が辺上にあるとする。
このとき、BQとCRが交わり、かつBP/PC・CQ/QA・AR/RB＝１が成り立つならば、
3直線AP、BQ、CRは1点で交わる。

Point2　例題
(1)　１辺の長さが７の正三角形ABCがある。辺AB、AC上にAD＝３、AE＝６となるように２点D、Eをとる。このとき、BE、CDの交点をF、直線AFとBCとの交点をGとする。CGの長さを求めよ。

(2)　△ABCの辺BC上に頂点と異なる点Dをとり、∠ADB、∠ADCの二等分線がAB、ACと交わる点をそれぞれE、Fとすると、AD、BF、CEは１点で交わることを証明せよ。

Point3　解答
(1)　条件より、AD/DB＝３/４、CE/EA＝１/６
チェバの定理より、　3/4・BG/GC・1/6＝１　　　よって　BG＝８GC
∴CG＝1/9BC＝７/９

(2)　DE、DFはそれぞれ∠ADB、∠ADCの二等分線であるから
　　　DA/DB＝AE/EB、DC/DA＝CF/FA
∴AE/EB・BD/DC・CF/FA＝DA/DB・BD/DC・DC/DA＝１
よって、チェバの定理の逆よりAD、BF、CEは1点で交わる。

Point1　基礎事項
メネラウスの定理

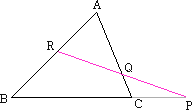
△ABCの辺BC、CA、ABまたはその延長が、三角形の頂点を通らない１直線とそれぞれ点P、Q、Rで交わるとき、
BP/PC・CQ/QA・AR/RB＝１　　　が成り立つ。

メネラウスの定理の逆
△ABCの辺BC、CA、ABまたはその延長線上に、それぞれ点P、Q、Rがあり、この３点のうちの１個または３個が辺の延長上にあるとする。
このとき、BP/PC・CQ/QA・AR/RB＝１ならば
P、Q、Rは１つの直線上にある。

Point2　例題
(1)　△ABCにおいて、辺AB上と辺ACの延長線上にそれぞれ点E、Fをとり、AE：EB＝１：２、AF：FC＝３：１とする。直線EFと直線BCとの交点をDとするとき、BD：DC、ED：DFを求めよ。

(2)　平行四辺形ABCD内の１点Pを通り、各辺に平行線を引き、辺AB、CD、BC、DAとの交点を順にQ、R、S、Tとする。２直線QS、RTが点Oで交わるとき、O、A、Cは１つの直線上にあることを示せ。

Point3　解答
(1)　BD：DC＝６：１　　　ED：DF＝４：３

(2)　

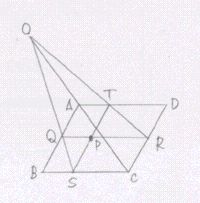
△PQSと直線OTRについて、メネラウスの定理より　QR/RP・PT/TS・SO/OQ＝１
PT＝AQ、TS＝AB、QR＝BC、PR＝CSであるから　BC/CS・AQ/AB・SO/OQ＝１
すなわち　　　QA/AB・BC/CS・SO/OQ＝１
よって、△BSQと３点O、A、Cについて、メネラウスの定理の逆より、３点O、A、Cは１つの直線上にある。