墌偲捈慄
Point1丂婎慴帠崁
愙慄偺挿偝
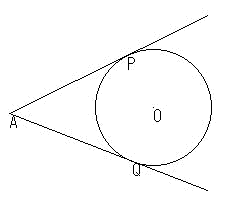
墌奜偺1揰A偐傜傂偄偨2杮偺愙慄偺挿偝偼摍偟偄丅
愙尫掕棟
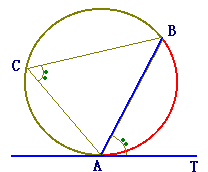
墌O偺尫AB偲偦偺抂揰A偵偍偗傞愙慄AT偑嶌傞佢BAT偺戝偒偝偼丄偦偺妏偺撪晹偵娷傑傟傞屖AB偵懳偡傞墌廃妏佢ACB偵摍偟偄丅
愙尫掕棟偺媡
墌O偺屖AB偲敿捈慄AT偑捈慄AB偺摨偠懁偵偁偭偰丄屖AB偵懳偡傞墌廃妏佢ACB偑佢BAT偵摍偟偄偲偒丄捈慄AT偼揰A偱墌O偵愙偡傞丅
Point2丂椺戣
侾丏壓偺恾偺傛偆偵丄墌O偵撪愙偡傞仮ABC偑偁傞丅揰C偵偍偗傞墌O偺愙慄偲AB偺墑挿偲偺岎揰傪P偲偡傞丅傑偨丄揰P傪捠傝BC偵暯峴側捈慄偲AC偺墑挿偲偺岎揰傪Q偲偡傞丅偨偩偟AC亜BC偲偡傞丅
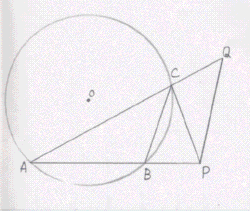
乮1乯丂仮ABC佷仮PCQ偱偁傞偙偲傪徹柧偣傛丅
乮2乯丂CQ亖係丄PQ亖俈偺偲偒丄BC偺挿偝傪媮傔傛丅
俀丏墌O偺奜晹偺揰P偐傜偙偺墌偵愙慄PA丄PB傪堷偔丅揰B傪捠傝丄PA偲暯峴側捈慄偑墌O偲嵞傃岎傢傞揰傪C偲偡傞偲偒
乮1乯丂捈慄AC偼仮PAB偺奜愙墌偺愙慄偱偁傞偙偲傪徹柧偣傛丅
乮2乯丂佢PAC亖114亱偱偁傞偲偒丄佢PBC偺戝偒偝傪媮傔傛丅
Point3丂夝摎
侾丏乮侾乯
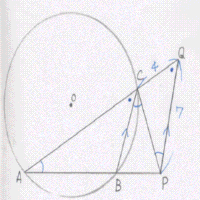
仮ABC偲仮PCQ偵偍偄偰丄BC//PQ偐傜
佢ACB亖佢PQC乧嘆
傑偨丂佢BCP亖佢CPQ丄佢BCP亖佢BAC
傛偭偰丂佢BAC亖佢CPQ乧嘇
嘆丄嘇傛傝仮ABC佷仮PCQ
乮俀乯丂仮ABC佷仮APQ偐傜丂仮APQ佷仮PCQ
傛偭偰PQ丗CQ亖AQ丗PQ偱偁傞偐傜丂俈丗係亖AQ丗俈
亪AQ亖49/4
傑偨丄BC//PQ偐傜BC丗PQ亖AC丗AQ
偙偙偱丂AC丗AQ亖33丗49
傛偭偰丄BC丗俈亖俁俁丗係俋偐傜丂BC亖33/7
俀丏乮侾乯
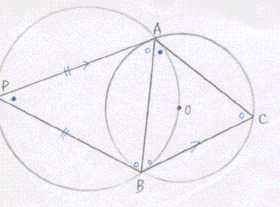
恾偱丄佢ABC亖a偲偡傞丅
PA//BC偐傜丂佢PAB亖佢ABC亖a乮嶖妏乯
PA亖PB偐傜丂佢PAB亖佢PBA亖a
傛偭偰丄仮APB偱丂佢APB亖180亱亅2a乧嘆
傑偨丂佢ACB亖佢PBA亖a
傛偭偰丄仮ABC偱丂佢BAC亖180亱亅2a乧嘇
嘆嘇傛傝丂佢APB亖佢BAC
傛偭偰丄捈慄AC偼仮PAB偺奜愙墌偺愙慄偱偁傞丅
乮俀乯
佢PAC亖佢PAB亄佢BAC亖a亄180亱亅2a亖180亱亅a
亪180亱亅a亖114亱偐傜丂a亖66亱
傛偭偰丂佢PBC亖俀亊俇俇亱亖侾俁俀亱
愙慄偺挿偝

墌奜偺1揰A偐傜傂偄偨2杮偺愙慄偺挿偝偼摍偟偄丅
愙尫掕棟

墌O偺尫AB偲偦偺抂揰A偵偍偗傞愙慄AT偑嶌傞佢BAT偺戝偒偝偼丄偦偺妏偺撪晹偵娷傑傟傞屖AB偵懳偡傞墌廃妏佢ACB偵摍偟偄丅
愙尫掕棟偺媡
墌O偺屖AB偲敿捈慄AT偑捈慄AB偺摨偠懁偵偁偭偰丄屖AB偵懳偡傞墌廃妏佢ACB偑佢BAT偵摍偟偄偲偒丄捈慄AT偼揰A偱墌O偵愙偡傞丅
Point2丂
侾丏壓偺恾偺傛偆偵丄墌O偵撪愙偡傞仮ABC偑偁傞丅揰C偵偍偗傞墌O偺愙慄偲AB偺墑挿偲偺岎揰傪P偲偡傞丅傑偨丄揰P傪捠傝BC偵暯峴側捈慄偲AC偺墑挿偲偺岎揰傪Q偲偡傞丅偨偩偟AC亜BC偲偡傞丅

乮1乯丂仮ABC佷仮PCQ偱偁傞偙偲傪徹柧偣傛丅
乮2乯丂CQ亖係丄PQ亖俈偺偲偒丄BC偺挿偝傪媮傔傛丅
俀丏墌O偺奜晹偺揰P偐傜偙偺墌偵愙慄PA丄PB傪堷偔丅揰B傪捠傝丄PA偲暯峴側捈慄偑墌O偲嵞傃岎傢傞揰傪C偲偡傞偲偒
乮1乯丂捈慄AC偼仮PAB偺奜愙墌偺愙慄偱偁傞偙偲傪徹柧偣傛丅
乮2乯丂佢PAC亖114亱偱偁傞偲偒丄佢PBC偺戝偒偝傪媮傔傛丅
Point3
侾丏乮侾乯

仮ABC偲仮PCQ偵偍偄偰丄BC//PQ偐傜
佢ACB亖佢PQC乧嘆
傑偨丂佢BCP亖佢CPQ丄佢BCP亖佢BAC
傛偭偰丂佢BAC亖佢CPQ乧嘇
嘆丄嘇傛傝仮ABC佷仮PCQ
乮俀乯丂仮ABC佷仮APQ偐傜丂仮APQ佷仮PCQ
傛偭偰PQ丗CQ亖AQ丗PQ偱偁傞偐傜丂俈丗係亖AQ丗俈
亪AQ亖49/4
傑偨丄BC//PQ偐傜BC丗PQ亖AC丗AQ
偙偙偱丂AC丗AQ亖33丗49
傛偭偰丄BC丗俈亖俁俁丗係俋偐傜丂BC亖33/7
俀丏乮侾乯

恾偱丄佢ABC亖a偲偡傞丅
PA//BC偐傜丂佢PAB亖佢ABC亖a乮嶖妏乯
PA亖PB偐傜丂佢PAB亖佢PBA亖a
傛偭偰丄仮APB偱丂佢APB亖180亱亅2a乧嘆
傑偨丂佢ACB亖佢PBA亖a
傛偭偰丄仮ABC偱丂佢BAC亖180亱亅2a乧嘇
嘆嘇傛傝丂佢APB亖佢BAC
傛偭偰丄捈慄AC偼仮PAB偺奜愙墌偺愙慄偱偁傞丅
乮俀乯
佢PAC亖佢PAB亄佢BAC亖a亄180亱亅2a亖180亱亅a
亪180亱亅a亖114亱偐傜丂a亖66亱
傛偭偰丂佢PBC亖俀亊俇俇亱亖侾俁俀亱
br仺
main_box