Point1　基礎事項
方べきの定理
図１

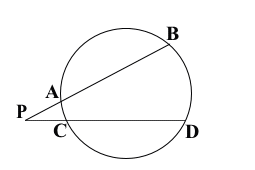
図２

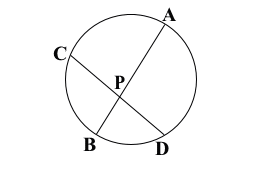
図３

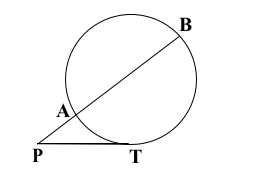
（図１、２）円の２つの弦AB、CDの交点、またはそれらの延長の交点をPとすると
　　　PA・PB＝PC・PD　　　が成り立つ。
（図３）円の外部の点Pから円に引いた接線の接点をTとする。Pを通ってこの円と2点A,Bで交わる直線を引くと、　　　PA・PB＝PT²

方べきの定理の逆
2つの線分AB、CD、またはそれらの延長の交点をPとするとき、
PA・PB＝PC・PDが成り立つならば、4点A、B、C、Dは1つの円周上にある。

Point2　例題
（1）　円に内接する四角形ABCDの対角線の交点EからADに平行線を引き、直線BCとの交点をFとする。Fからこの円に引いた接線FGの長さは線分FEの長さに等しいことを証明せよ。

（2）　交わる2円の交点Q、Rを通る直線上の点Pを通る2円の弦をそれぞれAB、CD（または割線をPAB、PCD）とするとき、A、B、C、Dは1つの円周上にあることを証明せよ。

Point3　解答
（1）　FE//ADであるから　∠ADB＝∠FEB
弧ABについて　∠ADB＝∠ACB
∠FEB＝∠ECBからFEは3点B、C、Eを通る円に接する。
よってFE²＝FB・FC
FGは円GBCの接線であるから　FG²＝FB・FC
したがって　FG＝FE

（2）　2円について
PA・PB＝PQ・PR
PC・PD＝PQ・PR
∴PA・PB＝PC・PD
よって、A、B、C、Dは1つの円周上にある。