Point1　基礎事項
�@組み合わせ　異なるn個のものの中から異なるr個を取る組み合わせの総数は

nCr=nPr/r!={n(n-1)(n-2)…(n-r+1)}/r(r-1)…3・2・1=n!/r!(n-r)!

特にnCn=1　ただしnP0=1,nC0=1と定める。
�AnCrの性質　[1]nCr=nCn-r(0≦r≦n)
　　　　　　　　　[2]nCr=n-1Cr+n-1Cr-1(1≦r≦n-1,n≧2)
�B同じものを含む順列　n個のもののうちp個は同じもの、q個は別の同じもの、r個はまた別の同じもの、…であるとき、それらn個のもの全部を使って作られる順列の総数はn!/p!q!r!　(p+q+r=n)

Point2　例題
Aを含む男子生徒5人、Bを含む女子生徒5人の計10人から5人を選ぶ。次のような方法は何通りあるか。
(1)全員から選ぶ選び方
(2)男子2人、女子3人を選ぶ選び方
(3)男子からAを含む2人、女子からBを含む3人を選ぶ選び方
(4)男子2人、女子3人を選んで1列に並べる並べ方

次の式を満たす自然数nを求めよ。ただし、n≧3とする。
6・nC3-n・nP2+144=0

A高校の生徒会の役員は6人で、そのうち3名は女子である。また、B高校の生徒会の役員は5名で、そのうち2名は女子である。各高校の役員から、それぞれ2名以上を出して、合計5名の合同委員会を作るとき、次の各場合は何通りあるか。
(1)合同委員会の作り方
(2)合同委員会に少なくとも1名女子が入っている場合
(3)合同委員会に1名女子が入っている場合

(1)円周上に異なる5点A,B,C,D,Eがあり、どの2点についてもそれを両端とする線分があるとする。
　(ｱ)線分は全部で何本あるか
　(ｲ)点Aが少なくとも1本の線分の端となるように線分を4本選ぶ方法は何通りあるか

(2)三角形の各辺を3分割したときの6点と3頂点のうちから3点を結んでできる三角形の個数は全部で何個あるか

9人を次のように分ける方法は何通りか。
(1)9人を4人、3人、2人の3組に分ける方法
(2)9人を3人ずつ、A,B,C3つの組に分ける方法
(3)9人を3人ずつ、3つの組に分ける方法

円盤の上面を4等分して(=それぞれの中心角は90度)隣り合う部分を異なる色で塗り分ける。回転して一致する塗り方は同じ塗り方として、次の場合の数を求めよ。
(1)赤、青、黄、緑の4色から2色を選び、塗り分ける場合の数
(2)赤、青、黄、緑の4色から3色を選び、3色全てを使って塗り分ける場合の数
(3)赤、青、黄、緑の4色以内で塗り分ける場合の数

internetの全ての文字を使ってできる順列のうち、どのtもどのeより左側にあるものは何通りか。

Point3　解答
(1)10C5=252通り

(2)5C2×5C3=100通り

(3)4C1×4C2=24通り

(4)(2)より、100×5!=12000通り

6・nC3-n・nP2+144=0…�@とおく。
nC3=n(n-1)(n-2)/3!,nP2=n(n-1)を�@に代入して、
n（n-1)(ｎ-2）−nの2乗(n-1)+144=0
整理するとnの2乗-n-72=0　ゆえに　(n+8)(n-9)=0
これを解いて、n≧3　から　n=9

(1)6C2×5C3+ 6C3×5C2=350通り

(2)全体から女子が1人もいない場合を引けばよい。 3C3×3C2=3通り
3C2×3C3=3通り
よって、350-(3+3)=344通り。

(3)女子1名がA高校の場合、男子の選び方は（A,B)=(2,2)、(1,3)であり、女子の選び方は3C1通りあるから　3C1(3C2×3C2 +3C1×3C3)=36通り
女子1名がB高校の場合、男子の選び方は（A,B)=(3,1)、(2,2)であり、女子の選び方は2C1通りであるから　2C1(3C3×3C1+ 3C2×3C2)=24通り
よって、36+24=60通り

(1)(ｱ)5C2=10本

(ｲ)(ｱ)の10本の線分から4本の線分を選ぶ方法の総数は10C4=210通り
また、端がAである線分は4本あるからどの線分の端も点Aでないように線分を4本選ぶ方法は　 10-4C4=15通り。よって210-15=195通り

(2)9点から3点を選ぶ方法は　9C3=84通り
このうち、各辺から3点を選ぶ方法は　3×4C3=12通り
よって　84-12=72個

(1)9C4×5C3×2C2=1260通り

(2)9C3×6C3×3C3=1680通り

(3)(9C3×6C3)/3!=280通り

(1)4C2=6通り

(2)3C1×4C1=12通り

(3)(4-1)!=6通り。よって、6+6+12=24通り

8!/4!2!=840通り

Point1　基礎事項
パスカルの三角形

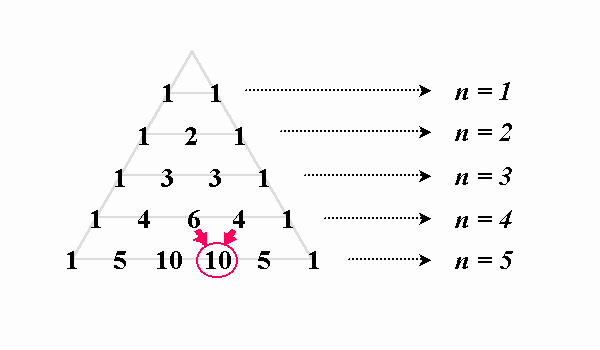
二項定理
(a+b)ⁿ=_nC₀aⁿ+_nC₁a^n-1b+_nC₂a^n-2b^２・・_nC_ra^n-rb^r・・・+_nC_nbⁿ

一般項(第r+1項)　_nC_ra^n-rb^r

多項定理
(a+b+c)ⁿの展開におけるa^pb^qc^rの係数は　
(n!/p!q!r!)×a^pb^qc^r　 　　　(p+q+r=n)

Point2　例題
次の式の展開式において[]内の項の係数を求めよ。
(1)(x+2)⁷ [x⁴]　 　　　(2)(x²-1)⁷ [x⁴,x³]　
(3)(x²+1/x)¹⁰ [x¹¹]　(4)(2x⁴-1/x)¹⁰ [定数項]

(1)(1+2a-3b)⁷の展開式におけるa²b³の係数を求めよ。
(2)(1+2a²+3/a)⁷の展開式におけるaの係数を求めよ。

Point3　解答
(1)₇C₃・2³=280
(2)₇C₅・(-1)⁵=-21[x⁴]
　整数rは存在しないので、x³の係数は0
(3)₁₀C₃=120
(4)₁₀C₈・2²=180

(1)(-1)³・7!/2!2!3!・2²・3³=-22680
(2)0≦p≦7より、q=1または2
　7!/5!1!1!・2・3+7!/2!2!3!・2²・3³=22932