嶰妏宍偲斾丒嶰妏宍偺屲怱
Point1丂婎慴帠崁
嶰妏宍偲斾
(1)丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(2)
 丂
丂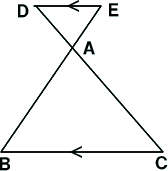
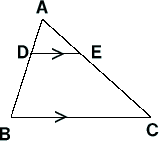
忋偺恾(1)偺仮ABC偵偍偄偰丄師偺傛偆側偙偲偑惉傝棫偮丅
[1]丂DE//BC佀AD丗AB亖AE丗AC亖DE丗BC
[2]丂AD丗DB亖AE丗EC
丂丂丂偙傟傜偺媡傕忢偵惉傝棫偮丅
偙偺掕棟偼恾(2)偺傛偆側恾宍偱傕惉傝棫偮丅
拞揰楢寢掕棟
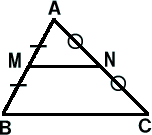
忋偺恾偺仮ABC偵偍偄偰丄AM亖MB丄AN亖NC側傜偽丄
[1]丂MN//BC
[2]丂MN亖1/2BC
Point2丂椺戣
(1)仮ABC偺曈AB丄AC忋偵丄偦傟偧傟捀揰偲堎側傞擟堄偺揰D丄E傪偲傞丅D偐傜BE偵暯峴偵丄傑偨丄E偐傜CD偵偵暯峴偵捈慄傪堷偒丄AC丄AB偲偺岎揰傪偦傟偧傟F丄G偲偡傞偲丄GF偼BC偵暯峴偱偁傞偙偲傪徹柧偣傛丅
(2)仮ABC偺曈BC忋偺揰P偵偮偄偰丄AB丗AC亖BP丗PC偑惉傝棫偮側傜偽AP偼佢A偺擇摍暘慄偱偁傞乧乧(*)
巐妏宍ABCD偺2偮偺撪妏佢A丄佢C偺擇摍暘慄偺岎揰偑丄懳妏慄BD忋偵偁傞側傜偽丄2偮偺撪妏佢B丄佢D偺擇摍暘慄偺岎揰傕懳妏慄AC忋偵偁傞偲偄偆偙偲傪丄(*)傪巊偭偰徹柧偣傛丅
Point3丂夝摎
(1)仮ABE偵偍偄偰丄DF//BE偱偁傞偐傜丂AD/AB=AF/AE乧嘆
丂仮ADC偵偍偄偰丄GE//DC偱偁傞偐傜丂AG/AD=AE/AC乧嘇
丂嘆偲嘇偺曈乆傪偐偗傞偲丂AD/AB丒AG/AD亖AF/AE丒AE/AC
丂亪AG/AB亖AF/AC
丂傛偭偰丂GF//BC
(2)佢A丄佢C偺擇摍暘慄偺岎揰傪E丄佢B偺擇摍暘慄偲AC偺岎揰傪F偲偡傞偲丄
丂AE丄CE偑偦傟偧傟丄佢A丄佢C偺擇摍暘慄偱偁傞偙偲偐傜
丂仮ABD偵偍偄偰丂AB/AD亖BE/DE丄仮BCD偵偍偄偰丂BC/CD亖BE/DE
丂亪丂AB/AD亖BC/CD丂偐傜丂AB/BC亖AD/CD乧嘆
丂BF偑佢B偺擇摍暘慄偱偁傞偙偲偐傜丂AF/CF亖BA/BC
丂傛偭偰丄嘆偐傜丂AF/CF亖AD/CD
丂偟偨偑偭偰丄(*)傛傝FD偼佢D偺擇摍暘慄偱偁傞丅
丂備偊偵丄寢榑偑惉傝棫偮丅
Point1丂婎慴帠崁
廳怱
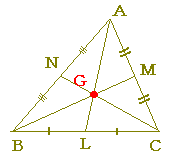
嶰妏宍偺3偮偺拞慄偼1揰偱岎傢傝丄偦偺揰偼奺拞慄傪俀丗侾偵撪暘偡傞
奜怱
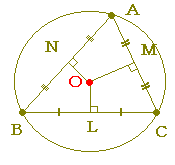
嶰妏宍偺俁曈偺悅捈擇摍暘慄偼侾揰偱岎傢傝丄偦偺揰傪拞怱偲偟偰奜愙墌偑偐偗傞
撪怱
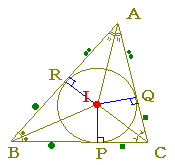
嶰妏宍偺俁偮偺撪妏偺擇摍暘慄偼侾揰偱岎傢傝丄偦偺揰傪拞怱偲偟偰撪愙墌偑偐偗傞
悅怱
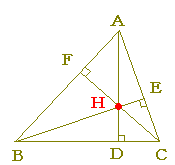
嶰妏宍偺奺捀揰偐傜懳曈傑偨偼偦偺墑挿偵壓傠偟偨悅慄偼侾揰偱岎傢傞
(徹柧)
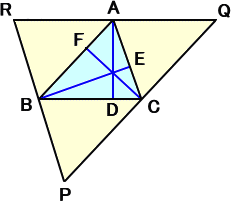
忋恾偺仮俙俛俠偵偍偄偰丄奺捀揰傪捠傝丄懳曈偵暯峴側慄暘傪堷偒丄仮俹俻俼傪嶌傞丅
丂偙偺偲偒丄俙偼曈俻俼偺拞揰偱丄俙俢偼曈俻俼偺悅慄偱偁傞丅
丂摨條偵丄俛偼曈俹俼偺拞揰偱丄俛俤偼曈俹俼偺悅慄偱偁傞丅
丂傛偭偰丄悅慄俙俢丄俛俤偺岎揰俫偼丄仮俹俻俼偺奜愙墌偺拞怱偱偁傞丅
丂偟偨偑偭偰丄曈俹俻偺悅捈擇摍暘慄俠俥偼丄揰俫傪捠傞丅
朤怱
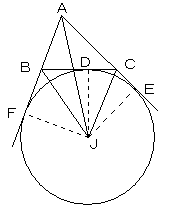
嶰妏宍偺侾曈偲巆傝偺俀曈偺墑挿忋偱愙偡傞墌傪朤愙墌偲偄偄丄偦偺拞怱傪朤怱偲偄偆仺仮俙俛俠偺佢俙偺妏偺擇摍暘慄偲丄佢俛丄佢俠偺奜妏乮曈俛俠偵懳偟偰丄揰俙偲斀懳懁偵庢傞乯偺俀摍暘慄偼堦揰偱岎傢傞丅
(徹柧)
曽恓仺佢俛偺奜妏偺擇摍暘慄偲丄佢俠偺奜妏偺擇摍暘慄偺岎揰俰傪峫偊傞丅
揰俰偐傜丄俛俠丆俠俙丆俙俛偵偍傠偟偨悅慄偺懌傪丄俢丆俤丆俥偲偡傞丅
撪怱偺帪偲摨條偵丄俰俥亖俰俢 偍傛傃丄俰俢亖俰俤 傛傝丄
丂俰俥亖俰俤乧嘆
偲側傝丄仮俰俙俥偲仮俰俙俤偵偍偄偰丄
丂JF亖JE乧嘆
丂佢俙俥俰亖佢俙俤俰亖俋侽亱乧嘇
丂幬曈偼嫟捠乧嘊
嘆嘇嘊傛傝丄仮俰俙俥偲仮俰俙俤偼崌摨偱偁傝丄俙俰偼佢俛俙俠偺擇摍暘慄偲側傞丅
埲忋傛傝丄佢俙偺擇摍暘慄偲丄佢俛丄佢俠偺奜妏偺擇摍暘慄偼堦揰俰偱岎傢傞丅
Point2丂椺戣
仮ABC偺奜怱傪O丄悅怱傪H偲偟丄O偐傜曈BC偵壓傠偟偨悅慄傪OM偲偡傞偲丄
AH亖俀OM偱偁傞偙偲傪徹柧偣傛丅
(1)丂仮ABC偺曈AB丄AC忋偵偦傟偧傟捀揰偲堎側傞揰D丄E傪偲傞偲偒
仮ADE/仮ABC亖AD/AB丒AE/AC偑惉傝棫偮帠傪徹柧偣傛丅
(2)丂仮ABC偺曈BC丄CA丄AB傪俁丗俀偵撪暘偡傞揰傪偦傟偧傟D丄E丄F偲偡傞丅仮ABC偲仮DEF偺柺愊斾傪媮傔傛丅
Point3丂夝摎
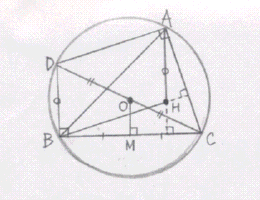
仮ABC偺奜愙墌偲捈慄OC偲偺岎揰傪D偲偡傞偲丄M偼曈BC偺拞揰丄O偼慄暘DC偺拞揰偱偁傞偐傜丄拞揰楢寢掕棟傛傝丂丂丂DB亖俀OM乧嘆
慄暘CD偼奜愙墌偺捈宎偱偁傞偐傜丂DB佦BC丄AH佦BC傛傝丂丂丂DB//AH
DA佦AC丄BH佦AC傛傝丂丂丂DA//BH
亪巐妏宍ADBH偼暯峴巐曈宍偱偁傞丅
傛偭偰丂丂丂AH亖DB乧嘇
嘆嘇傛傝丂丂丂AH亖俀OM
乮侾乯
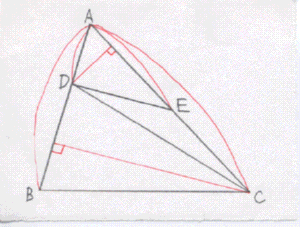
2揰C丄D傪寢傇丅
仮ADE偲仮ADC偼掙曈AE丄AC偐傜偺崅偝偑摍偟偄偐傜
仮ADE/仮ADC亖AE/AC乧嘆
仮ADC偲仮ABC偼掙曈AD丄AB偐傜偺崅偝偑摍偟偄偐傜
仮ADC/仮ABC亖AD/AB乧嘇
嘆丄嘇偺曈傌傫傪偐偗傞偲丂丂丂AE/AC丒AD/AB
亪仮ADE/仮ADC丒仮ADC/仮ABC亖AD/AB丒AE/AC
乮俀乯
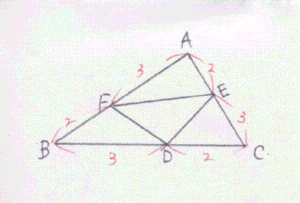
乮侾乯傛傝丂仮AFE/仮ABC亖AF/AB丒AE/AC亖乮俁/俆乯丒(俀/俆)亖俇/俀俆
仮BDF/仮ABC亖俇/俀俆
仮CED/仮ABC亖俇/俀俆
偙偙偱丂仮DEF亖仮ABC亅仮AFE亅仮BDF亅仮CED
椉曈傪仮ABC偱妱傞偲
仮DEF/仮ABC亖侾亅俇/俀俆亅俇/俀俆亅俇/俀俆亖俈/俀俆
亪仮ABC丗仮DEF亖俀俆丗俈
嶰妏宍偲斾
(1)丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂(2)
 丂
丂
忋偺恾(1)偺仮ABC偵偍偄偰丄師偺傛偆側偙偲偑惉傝棫偮丅
[1]丂DE//BC佀AD丗AB亖AE丗AC亖DE丗BC
[2]丂AD丗DB亖AE丗EC
丂丂丂偙傟傜偺媡傕忢偵惉傝棫偮丅
偙偺掕棟偼恾(2)偺傛偆側恾宍偱傕惉傝棫偮丅
拞揰楢寢掕棟

忋偺恾偺仮ABC偵偍偄偰丄AM亖MB丄AN亖NC側傜偽丄
[1]丂MN//BC
[2]丂MN亖1/2BC
Point2丂
(1)仮ABC偺曈AB丄AC忋偵丄偦傟偧傟捀揰偲堎側傞擟堄偺揰D丄E傪偲傞丅D偐傜BE偵暯峴偵丄傑偨丄E偐傜CD偵偵暯峴偵捈慄傪堷偒丄AC丄AB偲偺岎揰傪偦傟偧傟F丄G偲偡傞偲丄GF偼BC偵暯峴偱偁傞偙偲傪徹柧偣傛丅
(2)仮ABC偺曈BC忋偺揰P偵偮偄偰丄AB丗AC亖BP丗PC偑惉傝棫偮側傜偽AP偼佢A偺擇摍暘慄偱偁傞乧乧(*)
巐妏宍ABCD偺2偮偺撪妏佢A丄佢C偺擇摍暘慄偺岎揰偑丄懳妏慄BD忋偵偁傞側傜偽丄2偮偺撪妏佢B丄佢D偺擇摍暘慄偺岎揰傕懳妏慄AC忋偵偁傞偲偄偆偙偲傪丄(*)傪巊偭偰徹柧偣傛丅
Point3
(1)仮ABE偵偍偄偰丄DF//BE偱偁傞偐傜丂AD/AB=AF/AE乧嘆
丂仮ADC偵偍偄偰丄GE//DC偱偁傞偐傜丂AG/AD=AE/AC乧嘇
丂嘆偲嘇偺曈乆傪偐偗傞偲丂AD/AB丒AG/AD亖AF/AE丒AE/AC
丂亪AG/AB亖AF/AC
丂傛偭偰丂GF//BC
(2)佢A丄佢C偺擇摍暘慄偺岎揰傪E丄佢B偺擇摍暘慄偲AC偺岎揰傪F偲偡傞偲丄
丂AE丄CE偑偦傟偧傟丄佢A丄佢C偺擇摍暘慄偱偁傞偙偲偐傜
丂仮ABD偵偍偄偰丂AB/AD亖BE/DE丄仮BCD偵偍偄偰丂BC/CD亖BE/DE
丂亪丂AB/AD亖BC/CD丂偐傜丂AB/BC亖AD/CD乧嘆
丂BF偑佢B偺擇摍暘慄偱偁傞偙偲偐傜丂AF/CF亖BA/BC
丂傛偭偰丄嘆偐傜丂AF/CF亖AD/CD
丂偟偨偑偭偰丄(*)傛傝FD偼佢D偺擇摍暘慄偱偁傞丅
丂備偊偵丄寢榑偑惉傝棫偮丅
Point1
廳怱

嶰妏宍偺3偮偺拞慄偼1揰偱岎傢傝丄偦偺揰偼奺拞慄傪俀丗侾偵撪暘偡傞
奜怱

嶰妏宍偺俁曈偺悅捈擇摍暘慄偼侾揰偱岎傢傝丄偦偺揰傪拞怱偲偟偰奜愙墌偑偐偗傞
撪怱

嶰妏宍偺俁偮偺撪妏偺擇摍暘慄偼侾揰偱岎傢傝丄偦偺揰傪拞怱偲偟偰撪愙墌偑偐偗傞
悅怱

嶰妏宍偺奺捀揰偐傜懳曈傑偨偼偦偺墑挿偵壓傠偟偨悅慄偼侾揰偱岎傢傞
(徹柧)

忋恾偺仮俙俛俠偵偍偄偰丄奺捀揰傪捠傝丄懳曈偵暯峴側慄暘傪堷偒丄仮俹俻俼傪嶌傞丅
丂偙偺偲偒丄俙偼曈俻俼偺拞揰偱丄俙俢偼曈俻俼偺悅慄偱偁傞丅
丂摨條偵丄俛偼曈俹俼偺拞揰偱丄俛俤偼曈俹俼偺悅慄偱偁傞丅
丂傛偭偰丄悅慄俙俢丄俛俤偺岎揰俫偼丄仮俹俻俼偺奜愙墌偺拞怱偱偁傞丅
丂偟偨偑偭偰丄曈俹俻偺悅捈擇摍暘慄俠俥偼丄揰俫傪捠傞丅
朤怱

嶰妏宍偺侾曈偲巆傝偺俀曈偺墑挿忋偱愙偡傞墌傪朤愙墌偲偄偄丄偦偺拞怱傪朤怱偲偄偆仺仮俙俛俠偺佢俙偺妏偺擇摍暘慄偲丄佢俛丄佢俠偺奜妏乮曈俛俠偵懳偟偰丄揰俙偲斀懳懁偵庢傞乯偺俀摍暘慄偼堦揰偱岎傢傞丅
(徹柧)
曽恓仺佢俛偺奜妏偺擇摍暘慄偲丄佢俠偺奜妏偺擇摍暘慄偺岎揰俰傪峫偊傞丅
揰俰偐傜丄俛俠丆俠俙丆俙俛偵偍傠偟偨悅慄偺懌傪丄俢丆俤丆俥偲偡傞丅
撪怱偺帪偲摨條偵丄俰俥亖俰俢 偍傛傃丄俰俢亖俰俤 傛傝丄
丂俰俥亖俰俤乧嘆
偲側傝丄仮俰俙俥偲仮俰俙俤偵偍偄偰丄
丂JF亖JE乧嘆
丂佢俙俥俰亖佢俙俤俰亖俋侽亱乧嘇
丂幬曈偼嫟捠乧嘊
嘆嘇嘊傛傝丄仮俰俙俥偲仮俰俙俤偼崌摨偱偁傝丄俙俰偼佢俛俙俠偺擇摍暘慄偲側傞丅
埲忋傛傝丄佢俙偺擇摍暘慄偲丄佢俛丄佢俠偺奜妏偺擇摍暘慄偼堦揰俰偱岎傢傞丅
Point2丂
仮ABC偺奜怱傪O丄悅怱傪H偲偟丄O偐傜曈BC偵壓傠偟偨悅慄傪OM偲偡傞偲丄
AH亖俀OM偱偁傞偙偲傪徹柧偣傛丅
(1)丂仮ABC偺曈AB丄AC忋偵偦傟偧傟捀揰偲堎側傞揰D丄E傪偲傞偲偒
仮ADE/仮ABC亖AD/AB丒AE/AC偑惉傝棫偮帠傪徹柧偣傛丅
(2)丂仮ABC偺曈BC丄CA丄AB傪俁丗俀偵撪暘偡傞揰傪偦傟偧傟D丄E丄F偲偡傞丅仮ABC偲仮DEF偺柺愊斾傪媮傔傛丅
Point3

仮ABC偺奜愙墌偲捈慄OC偲偺岎揰傪D偲偡傞偲丄M偼曈BC偺拞揰丄O偼慄暘DC偺拞揰偱偁傞偐傜丄拞揰楢寢掕棟傛傝丂丂丂DB亖俀OM乧嘆
慄暘CD偼奜愙墌偺捈宎偱偁傞偐傜丂DB佦BC丄AH佦BC傛傝丂丂丂DB//AH
DA佦AC丄BH佦AC傛傝丂丂丂DA//BH
亪巐妏宍ADBH偼暯峴巐曈宍偱偁傞丅
傛偭偰丂丂丂AH亖DB乧嘇
嘆嘇傛傝丂丂丂AH亖俀OM
乮侾乯

2揰C丄D傪寢傇丅
仮ADE偲仮ADC偼掙曈AE丄AC偐傜偺崅偝偑摍偟偄偐傜
仮ADE/仮ADC亖AE/AC乧嘆
仮ADC偲仮ABC偼掙曈AD丄AB偐傜偺崅偝偑摍偟偄偐傜
仮ADC/仮ABC亖AD/AB乧嘇
嘆丄嘇偺曈傌傫傪偐偗傞偲丂丂丂AE/AC丒AD/AB
亪仮ADE/仮ADC丒仮ADC/仮ABC亖AD/AB丒AE/AC
乮俀乯

乮侾乯傛傝丂仮AFE/仮ABC亖AF/AB丒AE/AC亖乮俁/俆乯丒(俀/俆)亖俇/俀俆
仮BDF/仮ABC亖俇/俀俆
仮CED/仮ABC亖俇/俀俆
偙偙偱丂仮DEF亖仮ABC亅仮AFE亅仮BDF亅仮CED
椉曈傪仮ABC偱妱傞偲
仮DEF/仮ABC亖侾亅俇/俀俆亅俇/俀俆亅俇/俀俆亖俈/俀俆
亪仮ABC丗仮DEF亖俀俆丗俈
br仺
main_box