Point1　基礎事項
有効線分とベクトル

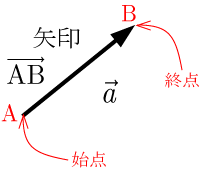
有効線分AB　始点Aから終点Bに向かう向きを指定した線分
ベクトル　向きと大きさだけで定まる量
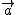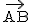
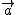　　　　　　＝　は有効線分ABの表すベクトル
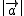　　ベクトル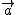の大きさ
単位ベクトル　大きさが１であるベクトル
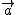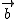
ベクトルの相当　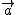＝　　と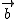の向きが同じで大きさが等しい。

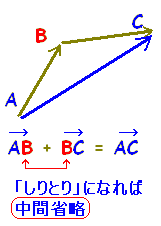
ベクトルの加法、減法、実数倍

�@　和　　　　　　　　　　　　　　　　　　�A　差
　　

�B　逆ベクトル　−

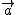
�C　零ベクトル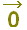　　　向きは考えない。

�D　実数倍

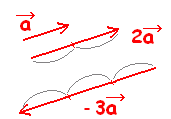
k = 2のとき
2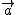は同じ向き2倍にしたもの
k = -3のとき
-3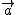は逆向きに|k| = |-3| = 3倍したもの。

→「ベクトルの実数倍は、

　k>0のとき同じ向きに、
　k<0のとき逆向きに

何倍かする。

ベクトルの演算法則
(a+b)+c = a+(b+c)
a+b = b+a
x・(y・a) = y・(x・a)
x・(a+b) = x・a+x・b

Point2　例題
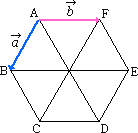　次のベクトルをいえ（図の、はきにしない）。
（１）　ABベクトルと等しいベクトル
（２）　EFベクトルの逆ベクトルと等しいベクトル
（３）　ACベクトルと等しいベクトル
（４）　ADベクトルと大きさが等しいベクトル
Point3　解答
（１）　EDベクトル　　　（２）　BCベクトル　　　（３）　FDベクトル
（４）　FCベクトル、DAベクトル、CFベクトル