仕事の原理と仕事率
Point1 基礎事項
物体に一定の大きさFの力がはたらいて、加えている力の向き(一直線上)に物体が距離x移動したとき、力Fと移動距離xとの積(Fx)をこの力が物体にした仕事Wという。
力Fも移動距離(変位)xもともにベクトルである。したがって、物体の移動する向きを正の向きとすれば、両者が同じ向きのとき、同一直線上のベクトルであるから、その成分の積である仕事Wは正の値をとる。
しかし、力と変位が反対向きのとき力の成分は−Fであり、仕事W=−Fxとなる。このときの力は負(−)の仕事をしたことになる。
また、力Fを加えても物体が移動しないときは、力は仕事をしていないことになる。
仕事の単位は、1Nの力がはたらいて、物体がその向きに1m移動したとき、この力のした仕事を単位の仕事量として 1ジュール(1J) という。
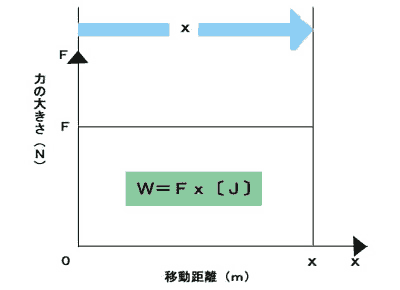
V-xグラフの面積は仕事量を表している。
Point2例題
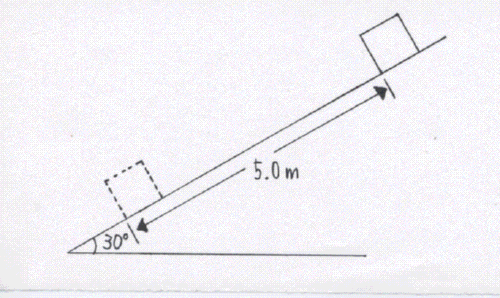
傾き30°のあらい斜面上に、質量2.0kgの物体を静かに置いた。物体が斜面に沿って5.0mすべりおりたときについて、以下の問いに答えよ。ただし、物体と斜面の間の動摩擦係数を0.30、重力加速度の大きさを9.8m/s2、√3=1.7とする。
(1) 以下の①〜③の力のする仕事(それらをW1〜W3とする)を求めよ。
① 重力 ② 動摩擦力 ③ 垂直抗力
(2) 物体にはたらく合力のする仕事Wを求めよ。
Point3 解答
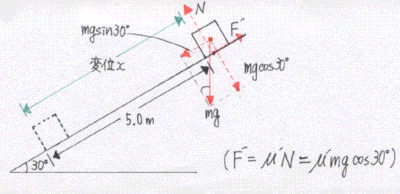
(1)① W1=mgsin30°×x=2.0×9.8×1/2×5.0=49(J)
② W2=−μ'N×x=−0.30×2.0×9.8×√3/2×5.0=−25(J)
③ W3=0(J)
(2) 合力F=mgsin30°−F'=mgsin30°−μ'mgcos30°
よって合力のする仕事W=Fx=mg(sin30°−μ'cos30°)×x
=2.0×9.8×(1/2−0.30×√3/2)×5.0=24(J)
Point1 基礎事項
滑らかな斜面に沿って質量m[kg]の物体を高さh[m]引き上げる場合、物体を引き上げる力がする仕事を考えよう。
斜面のけい角をθ[rad]とすると、物体にはたらく重力の斜面方向の分力はmgsinθ[N]となる。この力で物体を斜面に沿って引き上げることになるから、鉛直上向きに直接引き上げる場合(mg[N])に比べて小さい力ですむ。
しかし、高さh[m]引き上げるには、斜面上の移動距離l[m]は、h/sinθ[m]となって長くなり、斜面方向の分力のする仕事W[J]は
W=F・l=mgsinθ・h/sinθ=mgh
で、直接引き上げるときと同じ仕事量になる。
すなわち、斜面を利用して物体を上方へ引き上げる場合は小さい力ですむが、移動する距離が長くなり、結局仕事量は同じになる。
物体を重力に逆らって上方に引き上げるとき、機械を使って小さい力で行うことはできるが、仕事で得することはできない。これを仕事の原理という。
仕事の能率を表すには、1秒間当たりにする仕事の割合を用い、これを仕事率という。t[s]間にW[J]の仕事をするとき、仕事率Pは次式で表される。
仕事率の単位は、1秒間当たり1Jの仕事をする割合をとり1ワット(記号W)とする。また、物体がF[N]の力で一直線上を速さV[m/s]で進むとき、t[s]間にx[m]進めばV=x/t[m/s]である。このとき力Fのする仕事WはF・xであるから、仕事率Pは次のようになる。
Point2例題
(1) 質量80kgの荷物を、エレベータで20mの高さまで運ぶのに4.9秒かかった。エレベータの重力に逆らって荷物にした仕事の仕事率はいくらか。
(2) モーターボートが4.5×102Nの推進力で一直線上を一定の速さ4.0m/sで走っている。ボートにはたらいている水平方向の抵抗力(空気抵抗、水の抵抗などの合力)はいくらか。また、このときのエンジンの仕事率はいくらか。
Point3 解答
(1) エレベータが重力に逆らって荷物にした仕事Wは、
W=mgh=80×9.8×20=15680[J]
よって P=15680/4.9=3200=3.2×103[W]
(2) 加速度は0だから抵抗力=推進力=4.5×102[N]
したがってエンジンの仕事率P=FV=4.5×102×4.0=1.8[kW]
物体に一定の大きさFの力がはたらいて、加えている力の向き(一直線上)に物体が距離x移動したとき、力Fと移動距離xとの積(Fx)をこの力が物体にした仕事Wという。
| 重要 仕事量を求める公式 |
| W=Fx |
しかし、力と変位が反対向きのとき力の成分は−Fであり、仕事W=−Fxとなる。このときの力は負(−)の仕事をしたことになる。
また、力Fを加えても物体が移動しないときは、力は仕事をしていないことになる。
仕事の単位は、1Nの力がはたらいて、物体がその向きに1m移動したとき、この力のした仕事を単位の仕事量として 1ジュール(1J) という。
| 重要 仕事の単位 |
| 1J=1N・m |

V-xグラフの面積は仕事量を表している。
Point2

傾き30°のあらい斜面上に、質量2.0kgの物体を静かに置いた。物体が斜面に沿って5.0mすべりおりたときについて、以下の問いに答えよ。ただし、物体と斜面の間の動摩擦係数を0.30、重力加速度の大きさを9.8m/s2、√3=1.7とする。
(1) 以下の①〜③の力のする仕事(それらをW1〜W3とする)を求めよ。
① 重力 ② 動摩擦力 ③ 垂直抗力
(2) 物体にはたらく合力のする仕事Wを求めよ。
Point3

(1)① W1=mgsin30°×x=2.0×9.8×1/2×5.0=49(J)
② W2=−μ'N×x=−0.30×2.0×9.8×√3/2×5.0=−25(J)
③ W3=0(J)
(2) 合力F=mgsin30°−F'=mgsin30°−μ'mgcos30°
よって合力のする仕事W=Fx=mg(sin30°−μ'cos30°)×x
=2.0×9.8×(1/2−0.30×√3/2)×5.0=24(J)
Point1
滑らかな斜面に沿って質量m[kg]の物体を高さh[m]引き上げる場合、物体を引き上げる力がする仕事を考えよう。
斜面のけい角をθ[rad]とすると、物体にはたらく重力の斜面方向の分力はmgsinθ[N]となる。この力で物体を斜面に沿って引き上げることになるから、鉛直上向きに直接引き上げる場合(mg[N])に比べて小さい力ですむ。
しかし、高さh[m]引き上げるには、斜面上の移動距離l[m]は、h/sinθ[m]となって長くなり、斜面方向の分力のする仕事W[J]は
W=F・l=mgsinθ・h/sinθ=mgh
で、直接引き上げるときと同じ仕事量になる。
すなわち、斜面を利用して物体を上方へ引き上げる場合は小さい力ですむが、移動する距離が長くなり、結局仕事量は同じになる。
物体を重力に逆らって上方に引き上げるとき、機械を使って小さい力で行うことはできるが、仕事で得することはできない。これを仕事の原理という。
仕事の能率を表すには、1秒間当たりにする仕事の割合を用い、これを仕事率という。t[s]間にW[J]の仕事をするとき、仕事率Pは次式で表される。
| 仕事率の公式 |
| 仕事率P[W]=仕事量W[J]/時間t[s] |
仕事率の単位は、1秒間当たり1Jの仕事をする割合をとり1ワット(記号W)とする。また、物体がF[N]の力で一直線上を速さV[m/s]で進むとき、t[s]間にx[m]進めばV=x/t[m/s]である。このとき力Fのする仕事WはF・xであるから、仕事率Pは次のようになる。
| 仕事率 |
| P=W/t=F・x/t=FV |
Point2
(1) 質量80kgの荷物を、エレベータで20mの高さまで運ぶのに4.9秒かかった。エレベータの重力に逆らって荷物にした仕事の仕事率はいくらか。
(2) モーターボートが4.5×102Nの推進力で一直線上を一定の速さ4.0m/sで走っている。ボートにはたらいている水平方向の抵抗力(空気抵抗、水の抵抗などの合力)はいくらか。また、このときのエンジンの仕事率はいくらか。
Point3
(1) エレベータが重力に逆らって荷物にした仕事Wは、
W=mgh=80×9.8×20=15680[J]
よって P=15680/4.9=3200=3.2×103[W]
(2) 加速度は0だから抵抗力=推進力=4.5×102[N]
したがってエンジンの仕事率P=FV=4.5×102×4.0=1.8[kW]
br→
main_box