Point1　基礎事項
波源･･･最初に振動を起こした物質内の１点。
波（波動）･･･波源の振動が次々と伝わっていく現象。

　池の水面にできた波紋や紐を伝わる波の形は一般に曲線で表され、これを　波形　という。また、波を伝える物質を波の　媒質　という。


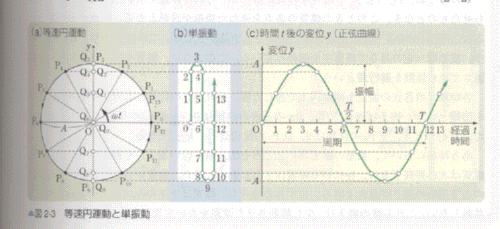
　図２−３（a）のように、物体が円周上を一定の速さで回る運動を　等速円運動　という。物体が１秒間に回る角度を　角速度　といい、　ω　で表す。角速度の単位は　ラジアン毎秒（rad/s）。
また、円を１周する時間T[s]を　周期　という。円の半径をA[m]、物体の速さをｖ[m/s]、角速度をω[rad/s]とすると、１回転での移動距離は円周２πA[m]、回転角は２π[rad]であるから、周期T[s]は次のように表される。

T　＝　２πA/ｖ　＝　２π/ω

一方、「弧の長さ＝半径×中心角」の関係から、ωとｖの間には次の関係式が成り立つ。

ｖ　＝　Aω

　等速円運動をする点Pの定直径上への正射影はQは、図２−３（ｂ）のように、直径上をOを中心として周期的に往復運動しているように見える。この運動を　単振動　という。横軸に経過時間ｔ、縦軸にQのOからの変位ｙをとると、グラフは同図（ｃ）のように　正弦曲線（サインカーブ）　を描く。Qの最大の変位（＝Pの円運動の半径）Aを　振幅　という。

位相･･･対応する円運動の中心角Θ→おもりが１周期の中のどの状態にあるかを示す。
山･･･ある時刻において、波形の最も高いところ。
谷･･･ある時刻において、波形の最も低いところ。

正弦波の動きは、　元の波形をかいてから、少し動かした波形をかいて考える　。



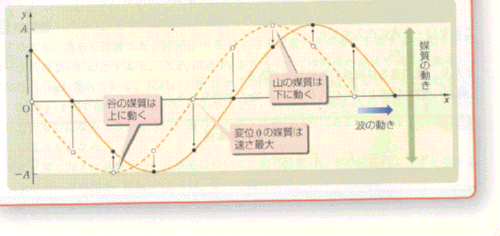
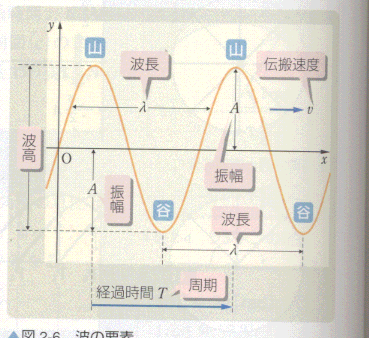
　同じ時刻に規則正しく繰り返し配列されている媒質の、同じ振動の状態（同位相）の隣り合う２点間の距離　λ　を　波長　という。また、振動の幅（山と谷の差）を　波高　、その半分（振動の中心からの最大変位）Aを　振幅　という。
　単位時間に媒質の１点を通過する波の数ｆを　波動の振動数　または　周波数　という。単位は　ヘルツ（Hz）　を用いる。

　波長λ[m]、周期T[s]の波動はT[s]間に１波長の距離を進むので、波の速さｖ[m/s]は次の式で表される。

ｖ　＝　λ/T　･･･（１）

また、１振動の時間がT[s]であるから、振動数ｆ[Hz]は１/Tとなる。すなわち

ｆ　＝　１/T　･･･（２）

これを（１）式に代入すると、

ｖ　＝　ｆλ

となり、波の速さは波長の振動数倍である。

横波（高低波）･･･波の進行方向⊥媒質の振動方向。
縦波（疎密波）･･･波の進行方向＝媒質の振動方向。



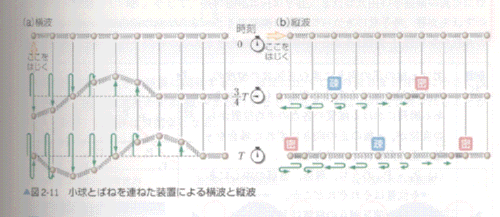
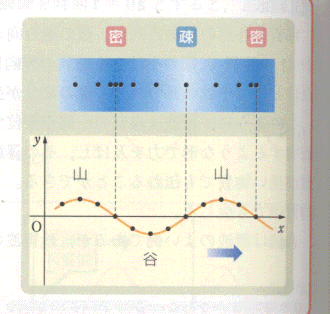
縦波の図示は、
�@　山から谷に向かう点が密部
�A　谷から山に向かう点が疎部

Point2　例題

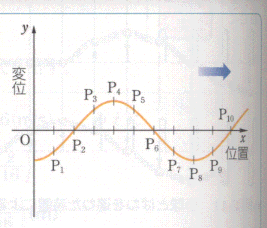
　図はｘ軸の正の向きに進む正弦波の縦波の、ある時刻における変位を表したものである。ある瞬間における媒質の各点の平均位置からの変位が、ｘ軸の正の向きにずれた場合をｙ軸の正の向きにとってある。
（１）　Ｐ₁〜Ｐ₁₀のうち、疎部、密部の中心にある位置はそれぞれどこか。
（２）　媒質の速さが０の位置はどこか。
（３）　媒質の速さが正の向きに最大の位置はどこか。
（４）　ある媒質内をこの縦波がｘ軸の正の向きに速さ８０ｃｍ/sで進行したとき、P₂,P₆,P₁₀の原点Oからの距離は、それぞれ２．０ｃｍ、６．０ｃｍ、１０ｃｍであった。この縦波の波長λ、振動数ｆを求めよ。

Point3　解答
（１）　波形の山から谷に向かう傾斜部の中点は密でP₆、谷から山に向かう部分の中点は疎でP₂,P₁₀
（２）　変位の最大点が媒質の振動の折り返し点で、速さは０となる。P₄,P₈
（３）　変位が０のところが速さが最大となる。波はｘ軸の正の向きに進むから、この後正の向きに変位するのはP₆
（４）　P2とP10間が１波長であるから
λ＝１０−２．０＝８．０ｃｍ　　　ｆ＝ｖ/λ＝８０/８．０＝１０Hz