重ね合わせの原理と波の干渉
Point1 基礎事項
媒質の1点が2つの波を同時に受けると、その点の変位は各波が単独に到達したときの変位を合成したものとなる。これを 波の重ね合わせの原理 という。
2つの波が重なり合う現象は、媒質の各点に2つの波の振動が同時に伝わるだけで、互いに他の波の進行を妨げたり、他の波に影響を与えたりはしない。これを 波の独立性 という。
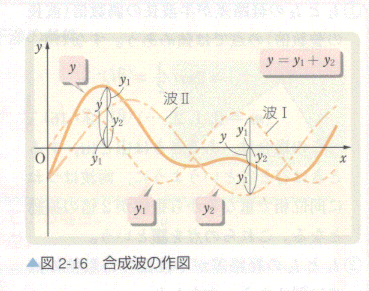
媒質の各点での、波Ⅰによる変位y1と波Ⅱによる変位y2の和が合成波の変位yとなる。
y = y1 + y2
波長の等しいいくつかの波が重なって、振動を強めあったり、弱めあったりする現象を 波の干渉 という。
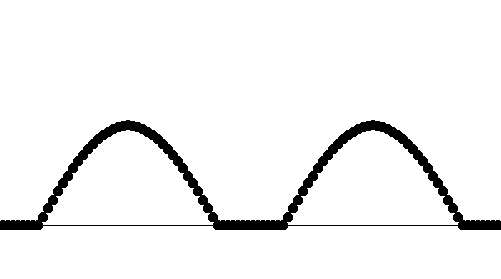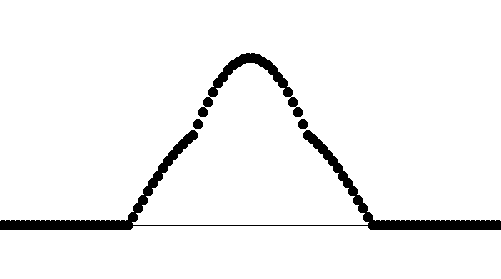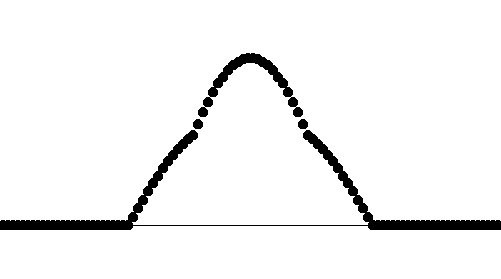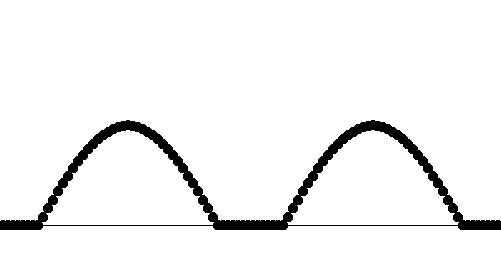
 このような波と、
このような波と、
 右に少しずらした波を
右に少しずらした波を
2つ重ね合わせると、
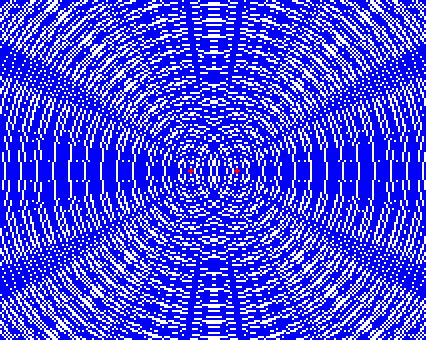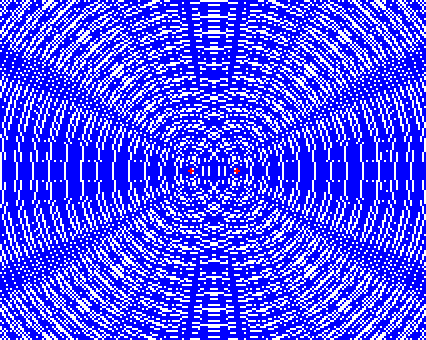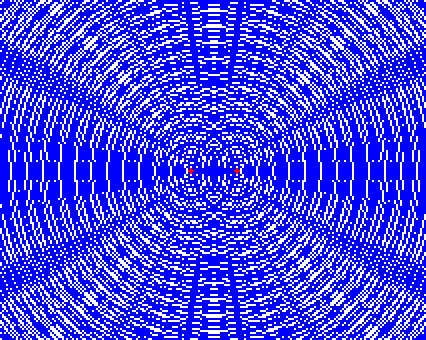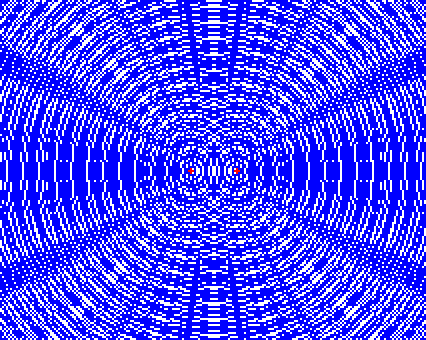 このような波が現れる。
このような波が現れる。
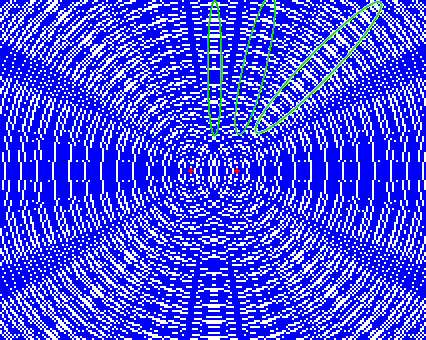
緑の部分は激しく振動する。このように、2つの波源から出た波が重なり合って強め合っている部分を 腹 という。
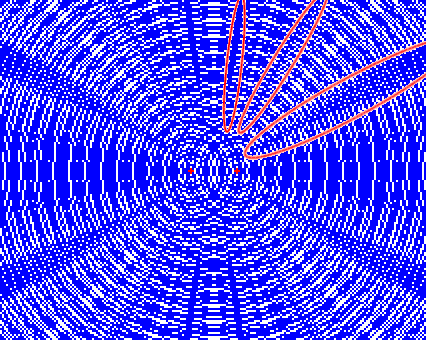
赤の部分は小さく振動する。このように、2つの波源から出た波が重なって弱まっている部分を 節 という。
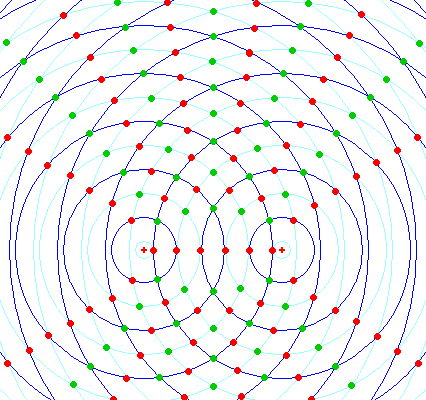
各場合の点をプロットすると次のようになる。
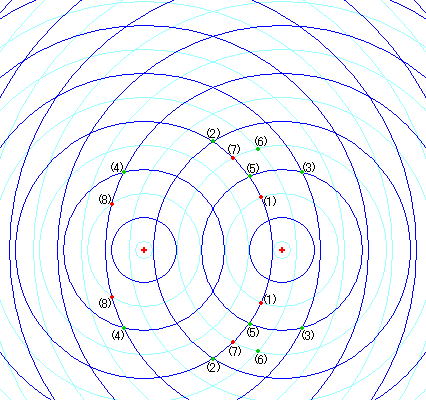
濃い青線が波の山、水色の線が波の谷で、強め合う地点は青線と青線又は水色線と水色線同士が重なり合っているところである。逆に弱めあう地点は青線と水色線が重なっているところである。
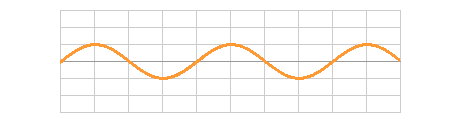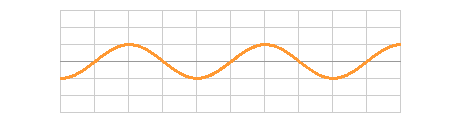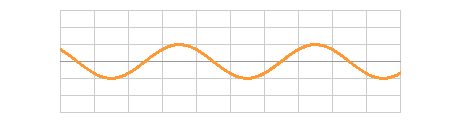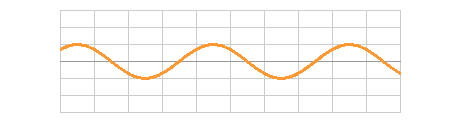
普通、波はゆれながら進んでいく。これを 進行波 という。
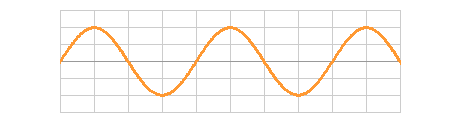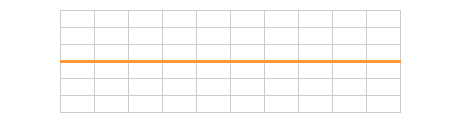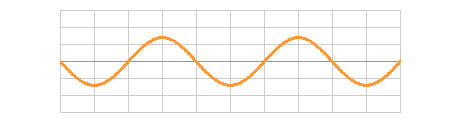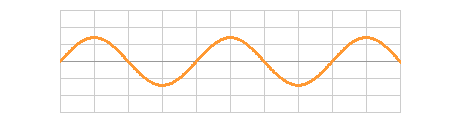
しかし、揺れてはいてもその場にとどまる波があり、このように波形の進まない一種の周期運動をする波を 定常波 という。

左右から波長、周期、振幅が等しい二つの進行波がやってきて真ん中でぶつかって重ね合わせの原理によって合成されると、その合成波は定常波になる。
Point2例題
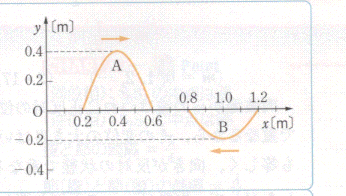
1. 図のように、正弦波のパルス波A,Bがx軸上をAは正の向き、Bは負の向きに0.1m/sの速さで進んでいる。2秒後と3秒後の合成波を作図せよ。ただし、パルス波Aの振幅はBの2倍である。
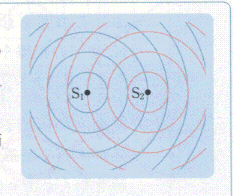
2. 浅く水をはった大きな水槽で、水面の2点S1、S2を同じ周期で同時にたたき、同じ振幅の2つの波をつくる。図の円、円弧はある瞬間における、それぞれの波の山の位置を示したものである。
(1) 2つの波が互いに弱めあう点を連ねる線(節線)は全部で何本できるか。
(2) 図に、示された範囲内の節線をすべて描け。
(3) 任意の節線上の1点をPとすると、PS1とPS2との間にはどのような関係があるか。
ただし、波長をλとする。
Point3 解答
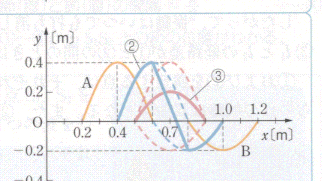
1. 下図の②が2秒後の、③が3秒後の合成波。
2.(1) 谷の位置を示す線を破線で記入する(図a)。
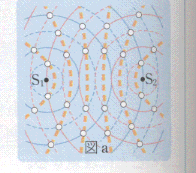
実線の円弧(山)と破線の円弧(谷)の交点(図aの○印)を連ねた曲線が節線となる。6本。
(2) 図a
(3) S1、S2は同位相であるから、距離の差が半波長の奇数倍のとき弱めあう。
|PS1-PS2|=(2m+1)λ/2=mλ+λ/2

媒質の1点が2つの波を同時に受けると、その点の変位は各波が単独に到達したときの変位を合成したものとなる。これを 波の重ね合わせの原理 という。
2つの波が重なり合う現象は、媒質の各点に2つの波の振動が同時に伝わるだけで、互いに他の波の進行を妨げたり、他の波に影響を与えたりはしない。これを 波の独立性 という。

媒質の各点での、波Ⅰによる変位y1と波Ⅱによる変位y2の和が合成波の変位yとなる。
y = y1 + y2
波長の等しいいくつかの波が重なって、振動を強めあったり、弱めあったりする現象を 波の干渉 という。
 このような波と、
このような波と、 右に少しずらした波を
右に少しずらした波を2つ重ね合わせると、
 このような波が現れる。
このような波が現れる。
緑の部分は激しく振動する。このように、2つの波源から出た波が重なり合って強め合っている部分を 腹 という。

赤の部分は小さく振動する。このように、2つの波源から出た波が重なって弱まっている部分を 節 という。
各場合の点をプロットすると次のようになる。

濃い青線が波の山、水色の線が波の谷で、強め合う地点は青線と青線又は水色線と水色線同士が重なり合っているところである。逆に弱めあう地点は青線と水色線が重なっているところである。

強め合う地点を緑、弱め合う地点を赤で全てプロットしてみると、図のような双曲線が現れる。緑の点のラインが(1)式を表し、赤の点のラインが(2)式を表している。
|l1-l2|=mλ (m=0,1,2,…) ・・・・・・(1)式、強め合う地点、腹の線。
|l1-l2|=(m+1/2)λ (m=0,1,2,…) ・・・・・・(2)式、弱め合う地点、節の線。
そして図の場合mは 0か1か2の三通りだけで、二つの波源がもっと離れていればmも 4、5、という値をとり、双曲線の本数も増える。| Point 波の干渉の条件 |
| 強めあう点 |l1-l2|=mλ 弱めあう点 |l1-l2|=mλ+λ/2 適用条件:波源が同位相で振動している場合。逆位相の場合は条件が逆。 節線の本数の見つけ方:節線の本数=線分S1S2上の節の数。 |

普通、波はゆれながら進んでいく。これを 進行波 という。

しかし、揺れてはいてもその場にとどまる波があり、このように波形の進まない一種の周期運動をする波を 定常波 という。

左右から波長、周期、振幅が等しい二つの進行波がやってきて真ん中でぶつかって重ね合わせの原理によって合成されると、その合成波は定常波になる。
| Point 定常波 |
| 腹と腹(節と節)の距離はλ/2 最大振幅は進行波の2倍、周期は進行波と同じ |
Point2

1. 図のように、正弦波のパルス波A,Bがx軸上をAは正の向き、Bは負の向きに0.1m/sの速さで進んでいる。2秒後と3秒後の合成波を作図せよ。ただし、パルス波Aの振幅はBの2倍である。

2. 浅く水をはった大きな水槽で、水面の2点S1、S2を同じ周期で同時にたたき、同じ振幅の2つの波をつくる。図の円、円弧はある瞬間における、それぞれの波の山の位置を示したものである。
(1) 2つの波が互いに弱めあう点を連ねる線(節線)は全部で何本できるか。
(2) 図に、示された範囲内の節線をすべて描け。
(3) 任意の節線上の1点をPとすると、PS1とPS2との間にはどのような関係があるか。
ただし、波長をλとする。
Point3
1. 下図の②が2秒後の、③が3秒後の合成波。

2.(1) 谷の位置を示す線を破線で記入する(図a)。

実線の円弧(山)と破線の円弧(谷)の交点(図aの○印)を連ねた曲線が節線となる。6本。
(2) 図a
(3) S1、S2は同位相であるから、距離の差が半波長の奇数倍のとき弱めあう。
|PS1-PS2|=(2m+1)λ/2=mλ+λ/2
br→
main_box