Point1　基礎事項
物体の運動の早い・遅いは平均の速度で見るととても分かり易い。

一般に平均の速さの公式は　v=x/t　で表される。

例えば、直線道路上を自動車が各時刻(t₁,t₂,t₃...)に定点Oからの距離(x₁,x₂,x₃...)の地点(A,B,C...)を通過したとき、この自動車のAB間の平均の速さは　v=(x₂-x₁)/(t₂-t₁)=x/t　(→単位時間当たりの平均移動距離=移動距離/要した時間)となる。

これが直線運動の基本的な考えの基となっている。

どの区間でも速さが一定の場合、その物体は　等速直線運動　をしている。

この運動の公式は　v=x/t=一定　となっている。

また、移動距離は　x=vt(vは一定)　となるので、v=一定から、xはvを比例定数としてtに比例することがわかる。更に、物体は常に等しい速度で運動し続けているため、　等速度運動　とも呼ばれる。ちなみに、運動のv-tグラフを書いた場合、そのグラフの面積は　移動距離x　の値を示す。

教科書P58の図9を見ると、曲線のグラフがある。x1に対するtの点をQ'とする。区間x1-x2での平均の速さは　v=(x2-x1)/(t2-t1)=QP/PQ'　となる。
これより　v=Δx/Δtという式で表せることがわかる。また、平均の速さを更に細かく区切って求めていくと一定の値に近づく。この極限の速さを　瞬間の速さ　という。ちなみにΔは変位を表す。

一般に「速度」というのは速さのみでとらえられがちだが、物理学的には「速さに向きをあわせたもの」が速度なのである。また、速度のように、大きさと向きをもつ量を一般に　ベクトル　という。一方、速さや温度、質量のように大きさだけで表される量を　スカラー　という。

A,Bの2物体が運動している時基準となる物体(観測者と表される事が多い)Aに対するBの速度を、Aに対するBの　相対速度　という。これは、Aから見たBの速度という意味。これを式で表すと　v_AB=v_B-v_A　となる。コツは　相手-自分　だと言う事。


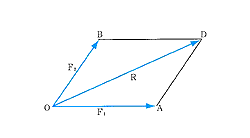
上の画像を例にしていうと、静水で速さV₁の船が、流水の速さV₂の川を横切って進むときの速度を考えると、はじめは点Oにあった船が船首を点Bに向けて進む。静水であれば船はOB上を進む。

しかし流水中では船は流されているため実際はOD間を進む。このとき、F₁+F₂=R。このODベクトル=Rベクトルを　F₁とF₂の合成ベクトル　という。

一般に、合成速度Vベクトルはそれぞれの速度V₁ベクトル、V₂ベクトルを２辺とする(ここではPベクトルとF₁ベクトルとF₂ベクトル)平行四辺形の対角線として求められる。これを　平行四辺形の法則　という。

また、この１つの速度Rベクトルは、合成の手順の逆により、２方向の２つの速度に分解できる。このときの分解の方法は何通りもある。
　　　　　Rベクトル=F1ベクトル+F2ベクトル

Point2　例題
直線道路上を2台の自動車A,Bが走っている。Aの速さが15m/s,Bの速さが10m/sのとき、次の場合についてAに対するBの相対速度をそれぞれ求めよ。
(1)A,Bが同じ向きに走る場合
(2)A,Bが反対向きに走る場合

Point3　解答
Aの進む向きを正とすると、
(1)v_AB=(+10)-(+15)=-5m/s　　 　　Aと反対向きに速さ5m/s
(2)v_AB=(-10)-(+15)=-25m/s　　　 Aと反対向きに速さ25m/s