作用・反作用の法則、運動の法則
Point1 基礎事項

このように、物体Aが物体Bに力FBベクトルをはたらかせると(作用)、反対にBはAに力FAベクトルを及ぼす(反作用)。これらの力の間には次のような関係がある。
①大きさが等しい
②作用線が共通である
③向きが反対である
FAベクトル=-FBベクトル
これを 作用・反作用の法則 という。
注意!!
作用・反作用とつりあいの2力を混同しないこと。つりあいの力は、1つの物体に対してはたらく2つの力であり、作用・反作用は別々の物体にはたらく2つの力である。
●力の見つけ方
接触していれば力を受ける→垂直抗力、摩擦力、張力、弾性力、浮力etc
接触していなくても力を受ける→重力、静電気力、磁気力など限られた力のみ。
○物体が複数あって、連結している場合→図を別々にかく。
Point2例題
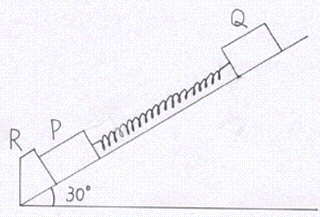
同じ質量mの物体P,Qが軽いばねで結ばれ、傾角30°のなめらかな斜面上に置かれている。斜面の下端には止め具Rがあり、Pは図のようにRに支えられて静止しており、ばねの長さはl1であった。次に、Qを斜面に沿って静かに引き上げたところ、ばねの長さがl2になったときにPがRから離れた。重力加速度の大きさをgとし、このばねの自然長l0とばね定数kを求めよ。
Point3 解答
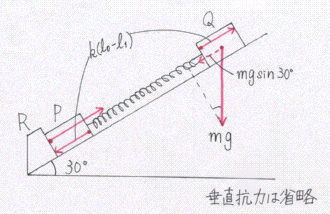
図(a)
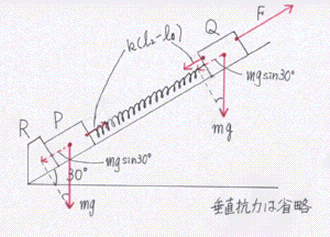
図(b)
図aで、ばねの縮みは(l0-l1)で、弾性力の大きさはk(l0-l1)であるから、Qについて、斜面方向の力のつり合いより k(l0-l1)-mgsin30°=0 …①
同様に、図bで、Pについての力のつりあいより k(l2-l0)-mgsin30°=0 …②
①、②式より l0=(l1+l2)/2, k=mg/(l2-l1)
Point1 基礎事項
静止状態の電車が急に発進すると、乗客は静止状態を続けようとして後方に倒れる。このようなことから、力がはたらかなければ物体はその状態を保ち続けようとする性質があると分かる。
すなわち 物体に外部から力がはたらかないとき、又はいくつかの力がはたらいていてもそれらの力が釣り合っているときは物体はいつまでも運動の状態を持続する。これを 慣性の法則 という。
止まっている物体はいつまでも静止を続け、動いている物体は等速直線運動を続ける。この性質を 慣性 という。
質量mの物体に力Fベクトルがはたらき加速度aベクトルを生じる時は次式が成立する
maベクトル=Fベクトル
力の単位ニュートンはこの関係式から導かれる。質量1kgの物体にFベクトルの力を加えて加速度1m/s2を得たとき、加えた力Fは F=1kg×1m/s2=1kg・m/s2 となり、
m[kg]・a[m/s2]=F[N]
この式を 運動方程式 といい、せまい意味での 運動の法則 という。
●ニュートンの運動の3法則
運動の第一法則…慣性の法則
運動の第二法則…運動の法則(運動方程式)
運動の第三法則…作用・反作用の法則
地上では常に物体は地球の中心の向きに力を受け、これを重力といった。また、物体が落下するときの加速度は、物体の重さに無関係であった。したがって、質量m[kg]の物体にはたらく重力の大きさW[N]は、運動方程式のaにgを、FにWを代入し、自由落下について運動方程式を立てることにより、
重力W=mg
と求められる。重力Wは質量mに比例する。質量m[kg]の物体は常にmg[N]の重力を鉛直下向きに受けており、それが物体の重さである。
○月面上での重さ
月面上の物体は月から重力を受ける。その重力は地球が地上の物体を引く力より弱く、月面での重力加速度は地上の重力加速度のおよそ1/6である。
質量→物質の量を表し、物体に固有のものでどこにあっても値が変わらない。
重さ→地球が物体を引く力の大きさで、場所によって値が異なる。
●連結(接触)した物体の運動方程式の立て方
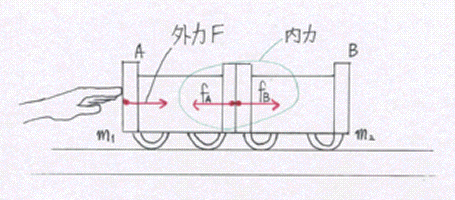
2通りの方法で加速度が求められる。
(1)物体1つ1つについてはたらく力を考慮して別々に運動方程式を立てる。
台車A,Bは一体となって走るのでその加速度は等しく、これをa[m/s2]とする。AにはF[N]とfA[N]の合力(F-fA)が、BにはfB[N]の力がはたらくので運動方程式は、
台車A:m1a=F-fA …① 台車B:m2a=fB …②
作用・反作用の法則よりfA=fBであるから、両式を加えると (m1+m2)a=F …③
ゆえに a=F/(m1+m2)[m/s2]
(2)物体系全体について運動方程式を立てる。
内力は考えないで外力だけを考えればよい。(1)の③式、すなわち(m1+m2)a=FはAとBをまとめて1つの物体と考えたときの運動方程式を表している。この式から直ちに加速度が求められる。このように、物体系全体の運動は外力F,全体の質量m1+m2で定まり、内力には関係がない。
Point2例題
(1)質量3.0kgの物体の重さは、地球上では何Nか。また、月面上だと何Nか。月面上における重力加速度の大きさは地球上の1/6倍とする。
(2)ある高さから小球を大きさVoの初速度で水平方向に投げたとき、どのような運動をするかを、水平・鉛直方向のそれぞれについて運動方程式を立てて示せ。
(3)
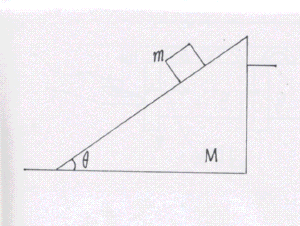
質量mの物体を、傾きθの斜面をもつ質量Mの台の上にのせる。台は図のように段差のある床に置かれている。物体を台の斜面上で静かに放すと、台は静止したまま物体が斜面を滑り降りた。
このときの物体の加速度の大きさa、物体と台の間にはたらく垂直抗力の大きさN、台が段差から水平方向に受ける力の大きさF、台が床から受ける垂直抗力の大きさN'をそれぞれ求めよ。
ただし、重力加速度の大きさをgとし、物体や台、床はなめらかで摩擦は全て無視できるものとする。
Point3 解答
(1)地球上では W=mg=3.0×9.8=29[N]
月面上では W'=mg'=3.0×9.8/6=4.9[N]
(2)小球の質量をm、水平方向をx、鉛直方向をyとする。
水平方向には力を受けず、鉛直方向に重力mgを受けるので、運動方程式は
水平方向:max=0 ゆえに ax=0
鉛直方向:may=mg ゆえに ay=g
水平方向には加速度ax=0で速度一定。初速度はVoであるから、速さVoの等速直線運動をする。→ Vx=Vo、 x=Vot
鉛直方向には、ay=gで加速度一定であるから、加速度の大きさgの等加速度直線運動をする。 → Vy=gt、 y=1/2gt2
(3)
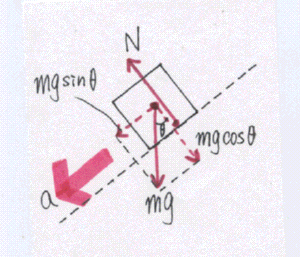
物体について斜面方向の運動方程式を立てると ma=mgsinθ …①
斜面と垂直な方向では力が釣り合っているので mgcosθ-N=0 …②
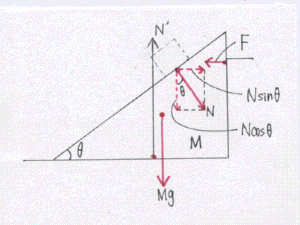
一方、台にはたらく力は釣り合っているので水平方向・鉛直方向についてそれぞれの力のつりあいの式を立てると
Nsinθ-F=0 …③
Ncosθ+Mg-N'=0 …④
①式より a=gsinθ
②式より N=mgcosθ
③、④式に求めたNを代入して
F=mgcosθsinθ、 N'=Mg+mgcos2θ

このように、物体Aが物体Bに力FBベクトルをはたらかせると(作用)、反対にBはAに力FAベクトルを及ぼす(反作用)。これらの力の間には次のような関係がある。
①大きさが等しい
②作用線が共通である
③向きが反対である
FAベクトル=-FBベクトル
これを 作用・反作用の法則 という。
注意!!
作用・反作用とつりあいの2力を混同しないこと。つりあいの力は、1つの物体に対してはたらく2つの力であり、作用・反作用は別々の物体にはたらく2つの力である。
●力の見つけ方
接触していれば力を受ける→垂直抗力、摩擦力、張力、弾性力、浮力etc
接触していなくても力を受ける→重力、静電気力、磁気力など限られた力のみ。
○物体が複数あって、連結している場合→図を別々にかく。
Point2

同じ質量mの物体P,Qが軽いばねで結ばれ、傾角30°のなめらかな斜面上に置かれている。斜面の下端には止め具Rがあり、Pは図のようにRに支えられて静止しており、ばねの長さはl1であった。次に、Qを斜面に沿って静かに引き上げたところ、ばねの長さがl2になったときにPがRから離れた。重力加速度の大きさをgとし、このばねの自然長l0とばね定数kを求めよ。
Point3

図(a)

図(b)
図aで、ばねの縮みは(l0-l1)で、弾性力の大きさはk(l0-l1)であるから、Qについて、斜面方向の力のつり合いより k(l0-l1)-mgsin30°=0 …①
同様に、図bで、Pについての力のつりあいより k(l2-l0)-mgsin30°=0 …②
①、②式より l0=(l1+l2)/2, k=mg/(l2-l1)
Point1
静止状態の電車が急に発進すると、乗客は静止状態を続けようとして後方に倒れる。このようなことから、力がはたらかなければ物体はその状態を保ち続けようとする性質があると分かる。
すなわち 物体に外部から力がはたらかないとき、又はいくつかの力がはたらいていてもそれらの力が釣り合っているときは物体はいつまでも運動の状態を持続する。これを 慣性の法則 という。
止まっている物体はいつまでも静止を続け、動いている物体は等速直線運動を続ける。この性質を 慣性 という。
質量mの物体に力Fベクトルがはたらき加速度aベクトルを生じる時は次式が成立する
maベクトル=Fベクトル
力の単位ニュートンはこの関係式から導かれる。質量1kgの物体にFベクトルの力を加えて加速度1m/s2を得たとき、加えた力Fは F=1kg×1m/s2=1kg・m/s2 となり、
m[kg]・a[m/s2]=F[N]
この式を 運動方程式 といい、せまい意味での 運動の法則 という。
●ニュートンの運動の3法則
運動の第一法則…慣性の法則
運動の第二法則…運動の法則(運動方程式)
運動の第三法則…作用・反作用の法則
地上では常に物体は地球の中心の向きに力を受け、これを重力といった。また、物体が落下するときの加速度は、物体の重さに無関係であった。したがって、質量m[kg]の物体にはたらく重力の大きさW[N]は、運動方程式のaにgを、FにWを代入し、自由落下について運動方程式を立てることにより、
重力W=mg
と求められる。重力Wは質量mに比例する。質量m[kg]の物体は常にmg[N]の重力を鉛直下向きに受けており、それが物体の重さである。
○月面上での重さ
月面上の物体は月から重力を受ける。その重力は地球が地上の物体を引く力より弱く、月面での重力加速度は地上の重力加速度のおよそ1/6である。
質量→物質の量を表し、物体に固有のものでどこにあっても値が変わらない。
重さ→地球が物体を引く力の大きさで、場所によって値が異なる。
●連結(接触)した物体の運動方程式の立て方

2通りの方法で加速度が求められる。
(1)物体1つ1つについてはたらく力を考慮して別々に運動方程式を立てる。
台車A,Bは一体となって走るのでその加速度は等しく、これをa[m/s2]とする。AにはF[N]とfA[N]の合力(F-fA)が、BにはfB[N]の力がはたらくので運動方程式は、
台車A:m1a=F-fA …① 台車B:m2a=fB …②
作用・反作用の法則よりfA=fBであるから、両式を加えると (m1+m2)a=F …③
ゆえに a=F/(m1+m2)[m/s2]
(2)物体系全体について運動方程式を立てる。
内力は考えないで外力だけを考えればよい。(1)の③式、すなわち(m1+m2)a=FはAとBをまとめて1つの物体と考えたときの運動方程式を表している。この式から直ちに加速度が求められる。このように、物体系全体の運動は外力F,全体の質量m1+m2で定まり、内力には関係がない。
| 重要!! 運動方程式とその立て方 |
| ma=F ①式を立てる物体の図を書く …質量(mなど)を側に記す ②力を書き込む …その物体にはたらく力だけを見落としなく ③加速度の矢印を書き込む …aなどを側に記す ④式を立てる ・・・「ma= 」の右辺に力を足し合わせていく |
Point2
(1)質量3.0kgの物体の重さは、地球上では何Nか。また、月面上だと何Nか。月面上における重力加速度の大きさは地球上の1/6倍とする。
(2)ある高さから小球を大きさVoの初速度で水平方向に投げたとき、どのような運動をするかを、水平・鉛直方向のそれぞれについて運動方程式を立てて示せ。
(3)

質量mの物体を、傾きθの斜面をもつ質量Mの台の上にのせる。台は図のように段差のある床に置かれている。物体を台の斜面上で静かに放すと、台は静止したまま物体が斜面を滑り降りた。
このときの物体の加速度の大きさa、物体と台の間にはたらく垂直抗力の大きさN、台が段差から水平方向に受ける力の大きさF、台が床から受ける垂直抗力の大きさN'をそれぞれ求めよ。
ただし、重力加速度の大きさをgとし、物体や台、床はなめらかで摩擦は全て無視できるものとする。
Point3
(1)地球上では W=mg=3.0×9.8=29[N]
月面上では W'=mg'=3.0×9.8/6=4.9[N]
(2)小球の質量をm、水平方向をx、鉛直方向をyとする。
水平方向には力を受けず、鉛直方向に重力mgを受けるので、運動方程式は
水平方向:max=0 ゆえに ax=0
鉛直方向:may=mg ゆえに ay=g
水平方向には加速度ax=0で速度一定。初速度はVoであるから、速さVoの等速直線運動をする。→ Vx=Vo、 x=Vot
鉛直方向には、ay=gで加速度一定であるから、加速度の大きさgの等加速度直線運動をする。 → Vy=gt、 y=1/2gt2
(3)


物体について斜面方向の運動方程式を立てると ma=mgsinθ …①
斜面と垂直な方向では力が釣り合っているので mgcosθ-N=0 …②
一方、台にはたらく力は釣り合っているので水平方向・鉛直方向についてそれぞれの力のつりあいの式を立てると
Nsinθ-F=0 …③
Ncosθ+Mg-N'=0 …④
①式より a=gsinθ
②式より N=mgcosθ
③、④式に求めたNを代入して
F=mgcosθsinθ、 N'=Mg+mgcos2θ
br→
main_box