Point1　基礎事項
静止物体を粗い面上に沿って動かそうとする力を加えたけど，動かない．これは物体が接する面から，面に沿った逆向きの抗力を受けるため．この抗力を　静止摩擦力　と言う．

静止摩擦力fは物体を面に沿って動かそうとする力の大きさによって異なるが，最大摩擦力F_mを越えることはできない．もし，動き出そうとするその時ならば，　最大静止摩擦力　となる．

静止摩擦力をμ，垂直抗力をNとするならば，最大摩擦力F_mは，
　　　　　F_m = μN　　　　　となる．
(発生例：床においてある大きな荷物を押してもなかなか動き出さないとき)

物体が粗い面を滑っているとき，物体は面から，滑る方向と逆向きに抗力を受ける．これを　動摩擦力　という．
動摩擦係数μ’を定める．垂直抗力をNとすれば動摩擦力F’は，
　　　　　F’ = μ’N
(発生例：自転車をこぐとき)

傾斜がθのあらい斜面上に質量Mの物体を置く。この傾斜θを0°(水平)からしだいに大きくしていくときある角度で物体は滑り落ち始める。このときの角度を　摩擦角　という。
tanθ=μ(静止摩擦係数)
補足；滑り出さない条件：F≦μN

Point2　例題

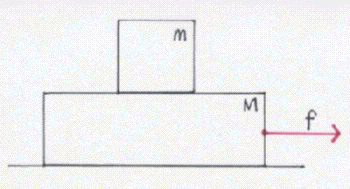
水平な床上に、質量Mの台を置き、その上に質量mの物体をのせる。台と床との間の摩擦は無視できる。台に右向きの力を加え、その力の大きさｆを０からしだいに大きくしていく。台と物体との間の静止摩擦係数をμ、動摩擦係数をμ’、重力加速度の大きさをｇとする。

(1)　fが小さい間は台と物体が一体となって動く。このときの加速度の大きさaと、台と物体の間にはたらく静止摩擦力の大きさＦを求めよ。
(2)台と物体が同じ速さで一体となって動くためにはfはいくら以下でなければならないか。
(3)fが大きくなって物体が台上を滑るときの物体の加速度a₁と台の加速度a₂を求めよ

Point3　解答
(1)

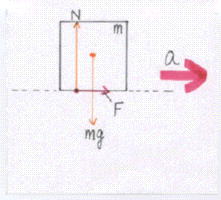
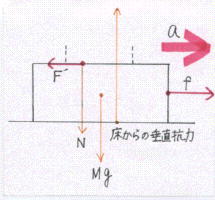
このときの運動方程式は　　　物体：ma=F　　　台：Ma=f-F
ゆえに　　　a=f/(m+M),　　　F=m/(m+M)f

(2)物体が台上を滑らないためには、Ｆ≦μＮ
　これに(1)で求めたＦと、Ｎ＝ｍｇを代入して　m/(m+M)f≦μmg
　ゆえに　　　f≦μ(m+M)g

(3)
　
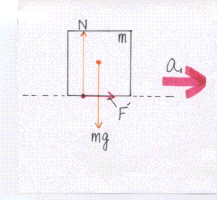
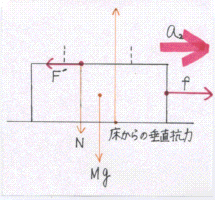
このときの運動方程式は　　　物体：ma₁=F'=μ’Ｎ　　　台：Ma₂=f-F'=f-μ'N
これらの式にN=mgを代入すると　　　a₁=μ'g,　a₂=(f-μ'mg)/M