キルヒホッフの第１法則
　交点aに流入する電流の総和は、点aから流出する電流の総和に等しい。

キルヒホッフの第２法則
　ある閉回路中に含まれる起電力（電源電圧）の総和は、その閉回路中にある
　電圧降下（端子電圧）の総和に等しい。


複雑な回路の電流の大きさと方向を求める方法…キルヒホッフの法則を使う
（例）P49の課題
R₁＝１００[Ω]、R₂＝２００[Ω]、R₃＝１００[Ω]、E₁＝６[V]、E₂＝１．５[V]


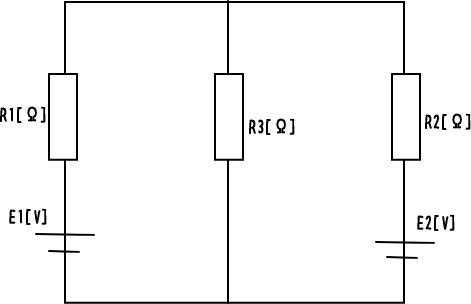
１．　まず、電流I₁、I₂、I₃の方向を仮設定（図のように決定）する。
　　　そして、計算のためにたどる輪（ループ）を仮設定する。（このとき、全ての
　　　部品にループが通るように複数のループを考える。



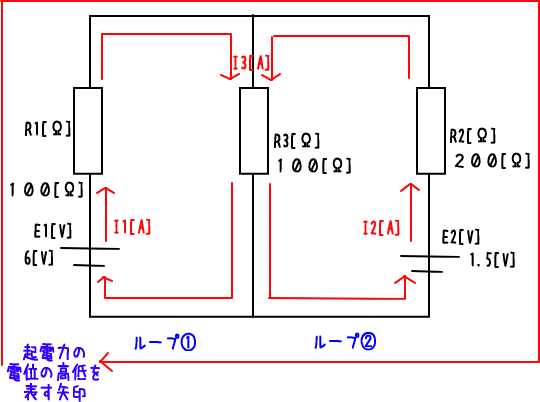
２．　キルヒホッフの法則にあてはめて計算する。
　キルヒホッフの第１法則より、　　　　　　　I₃＝I₁＋I₂…�@
　キルヒホッフの第２法則より、
　ループ�@について、E₁＝I₁R₁＋I₃R₃→６＝１００I₁＋１００I₃…�A
　ループ�Aについて、E₂＝I₂R₂＋I₃R₃→１．５＝２００I₂＋１００I₃…�B
　�@、�A、�Bを連立させて解くと、
　�A：I₃＝I₁＋I₂より、１００I₃＝１００I₁＋１００I₂
　　　∴６＝２００I₁＋１００I₂…�C
　�B：I₃＝I₁＋I₂より、１００I₃＝１００I₁＋１００I₂
　　　∴６＝１００I₁＋３００I₂…�D
　�C、�Dを連立させて解くと、答えが出る。
　A．I₁＝３３[mA]、I₂＝−６[mA]、I₃＝２７[mA]