交流回路の基礎
交流回路の基礎
(1)直流と交流
①直流(直流は、Direct currentを略してD.C.と表記します)
教科書P50の図3-1を参照。直流の定義は、「時間に対して符号(±)の変化が無い」という事。つまり、符号が変わらないという事は、電流の向きも変わらないって事です。 1学期の科技礎で、計算して出た値がマイナスになった場合、電流の向きも逆になると習ったよね?直流では、それが無い(起こらない)と言う事です。
直流回路を用いた代表的なものとしては乾電池や自動車のバッテリーなどです。
②交流(交流は、Alternating currenrを略してA.C.と表記します)
教科書P51の図3-2を参照。そのグラフをよく見てみると、電圧値がプラスだったりマイナスだったり波をうってます。交流の定義は、「時間に対して符号(±)が変化する(これをゼロクロスともいう)」という事。意味は言葉通り、電圧の値がプラスになったりマイナスになったりと正負の繰り返しになっています。
ちなみに、直流では記号は大文字、交流では小文字を用いる事になっています。また、一般家庭で使われているコンセント。これも交流です。
更に、教科書の図3-2のような波形をしている交流を「正弦波交流」といいます。それ以外の交流は「非正弦波交流」といいます。
現段階では、複雑になってしまうので単に「交流」といえばそれは「正弦波交流」を意味します。 「正弦」というのはご存知の通り「サイン、コサイン、タンジェント」のsinのことです。
グラフを見てください。波形の最も高い部分と最も低い部分に注目。ここでsin関数というのが登場するのですが、考え方は習ったとこと一緒。円を描いて、左回りに正として…っていうのを数理基礎でやったと思います。あれと似たように考えるんです。
半径が1の円だったとします。グラフの最も高い位置は、丁度半径が真上に伸びてるから「1」という数値になります。そして、グラフが下がって…「0」でストップ。(マイナスにはまだいかない)この時、sin関数で見るとsin180゜=0だから、この時(ゼロクロス)の値は「0」となります。次は更に下がって、グラフの最も低い部分に注目。sin270゜=-1と表せるので、この時の値は「-1」なんです。そして、上がって上がって…ゼロクロス。この時はsin360゜=0なので、この時の値は「0」になります。交流っていうのはこれの繰り返しと思えば大丈夫だと思います。
(2)交流(正弦波交流)の表し方
①瞬時値と最大値
・瞬時値
定義は「ある時刻における「瞬間」の値」となっています。言葉通りです。 瞬時値の集合が、波形です。要するに瞬時値が集まると、波の形が出来るんです。線は点と点の集まり、という事はわかりますよね?
・最大値
まず、さっき確認してもらった、sin90゜=1、sin270゜=-1 となる波形の最もプラスに大きい部分を見て下さい。要は、最大値とは「0[V]から見た最大の値、もとい瞬時値のうちで絶対値が最も大きいもの」のことをいいます。ここで勘違いしないでほしいのは、「最小値」というものは存在しません。0[V]からマイナスに向かって出来ている波のsin270゜=-1となる部分も、0[V]から見た最大の値となっている事を忘れないでください。
また、文字で表すとき、電圧の最大値をEm、電流の最大値をImで表します。添え字の「m」は、maximum(最大)の頭文字です。 この時、交流の電圧の瞬時値e[V]は、次のような式で求められます。
e=Em・sin(ωt+φ) [V]
(e:交流の電圧の瞬時値[V] Em:交流の電圧の最大値[V] ω:角速度[rad/s](ω=2πf) t:時間[s] φ:位相[rad])
この式は、Em=最大値、sin=関数、(ωt+φ)=関数に渡す値 という風に出来ています。 1年次では難しいのでファイは0と考えて良いそうです。
ここで「rad」という新しい単位が出てきました。radというのは角度の単位の事です。これは弧度法(単位円において、角度を円弧の長さで表す→360°=2πr、180°=π)で表します。まぁ現段階では特に気にしなくても良いでしょう。 ちなみに単位で考えると ωt=[rad/s]×[s]=rad となります。よって、現段階ではradの値だけ考えれば良いです。面倒くさいので公式だけ書きます。ここだけは、質問等は先生か分かる人に聞いて下さい。
ω=2πf[rad/s] (f=周波数[Hz])
・ピーク・ピーク値(peak to peak)
正の最大値から負の最大値までの値。普通、ピーク・ピーク値の半分が最大値である。これについては教科書の図3-4を参考にして下さい。 また、ピーク・ピーク値は電圧を Epp、電流を Ippで表します。
②周期と周波数
サイクルについては詳しくは教科書の図3-4を参照してください。
・周期…1サイクル(1周波)に要する時間。つまりsin0゜地点からsin360゜地点までって事ですね。(記号:T 単位[s])
・周波数…1秒間に何サイクルあるか(何回繰り返しているか)。(記号:f 単位[Hz])
周期Tと周波数fの関係式
f(周波数)=1/T [Hz]
例えば、関東を例にしてみましょう。関東エリアは50Hzの地域だという事は皆さんご存知だと思います。これを上の式に当てはめてみましょう。
f(周波数)=1/T →50=1/T 50T=1 T=1÷50=0,02[s]
という答えが導き出せるはずです。Tとは周期を表す記号なので、周期は0,02[s]です。これを、「マイクロメーター秒」に直してみましょう。1[ms]=0,001[s]なので、0,02[s]=20[ms]となります。
③平均値…半サイクルの平均
なぜ半サイクルなのか…それは、1サイクルの平均は当然0になるからです。(正の最大値と負の最大値の絶対値は等しい) また電圧の平均値をEa、電流の平均値をIaと表します。
交流の平均値と最大値の関係式
Ea(平均値)=(2/π)Em [V]br>
この関係式は正弦波交流の場合にしか通用しません。今のところはそんな事考えなくてOKです。
④実行値…交流の直流換算値?(そういう風に考える)
電圧はV、電流はIを用いて表します。
交流の実行値と最大値の関係式
実行値=(1/√2)×最大値[V]=Em/√2 [V]=Em=√2E
なお、交流の値は、特に断りの無い限り実行値で示す事になっています。 また、位相については試験範囲外なのでカットします。
レポート1
教科書P55.3.実験
(1)正弦波交流電圧の測定
結果はこちらの画像参照。
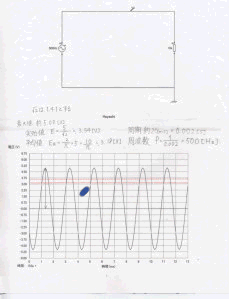
4.課題
①一般家庭のコンセントの交流電圧は実行値が100[V]である。最大値Em、平均値Ea[V]、およびピーク・ピーク値Epp[V]を求めよ。
答
最大値…Em=100√2=141
ピーク・ピーク値…Epp=282[V]
平均値…Ea=(2/π)141=282/π[V]
(1)直流と交流
①直流(直流は、Direct currentを略してD.C.と表記します)
教科書P50の図3-1を参照。直流の定義は、「時間に対して符号(±)の変化が無い」という事。つまり、符号が変わらないという事は、電流の向きも変わらないって事です。 1学期の科技礎で、計算して出た値がマイナスになった場合、電流の向きも逆になると習ったよね?直流では、それが無い(起こらない)と言う事です。
直流回路を用いた代表的なものとしては乾電池や自動車のバッテリーなどです。
②交流(交流は、Alternating currenrを略してA.C.と表記します)
教科書P51の図3-2を参照。そのグラフをよく見てみると、電圧値がプラスだったりマイナスだったり波をうってます。交流の定義は、「時間に対して符号(±)が変化する(これをゼロクロスともいう)」という事。意味は言葉通り、電圧の値がプラスになったりマイナスになったりと正負の繰り返しになっています。
ちなみに、直流では記号は大文字、交流では小文字を用いる事になっています。また、一般家庭で使われているコンセント。これも交流です。
更に、教科書の図3-2のような波形をしている交流を「正弦波交流」といいます。それ以外の交流は「非正弦波交流」といいます。
現段階では、複雑になってしまうので単に「交流」といえばそれは「正弦波交流」を意味します。 「正弦」というのはご存知の通り「サイン、コサイン、タンジェント」のsinのことです。
グラフを見てください。波形の最も高い部分と最も低い部分に注目。ここでsin関数というのが登場するのですが、考え方は習ったとこと一緒。円を描いて、左回りに正として…っていうのを数理基礎でやったと思います。あれと似たように考えるんです。
半径が1の円だったとします。グラフの最も高い位置は、丁度半径が真上に伸びてるから「1」という数値になります。そして、グラフが下がって…「0」でストップ。(マイナスにはまだいかない)この時、sin関数で見るとsin180゜=0だから、この時(ゼロクロス)の値は「0」となります。次は更に下がって、グラフの最も低い部分に注目。sin270゜=-1と表せるので、この時の値は「-1」なんです。そして、上がって上がって…ゼロクロス。この時はsin360゜=0なので、この時の値は「0」になります。交流っていうのはこれの繰り返しと思えば大丈夫だと思います。
(2)交流(正弦波交流)の表し方
①瞬時値と最大値
・瞬時値
定義は「ある時刻における「瞬間」の値」となっています。言葉通りです。 瞬時値の集合が、波形です。要するに瞬時値が集まると、波の形が出来るんです。線は点と点の集まり、という事はわかりますよね?
・最大値
まず、さっき確認してもらった、sin90゜=1、sin270゜=-1 となる波形の最もプラスに大きい部分を見て下さい。要は、最大値とは「0[V]から見た最大の値、もとい瞬時値のうちで絶対値が最も大きいもの」のことをいいます。ここで勘違いしないでほしいのは、「最小値」というものは存在しません。0[V]からマイナスに向かって出来ている波のsin270゜=-1となる部分も、0[V]から見た最大の値となっている事を忘れないでください。
また、文字で表すとき、電圧の最大値をEm、電流の最大値をImで表します。添え字の「m」は、maximum(最大)の頭文字です。 この時、交流の電圧の瞬時値e[V]は、次のような式で求められます。
e=Em・sin(ωt+φ) [V]
(e:交流の電圧の瞬時値[V] Em:交流の電圧の最大値[V] ω:角速度[rad/s](ω=2πf) t:時間[s] φ:位相[rad])
この式は、Em=最大値、sin=関数、(ωt+φ)=関数に渡す値 という風に出来ています。 1年次では難しいのでファイは0と考えて良いそうです。
ここで「rad」という新しい単位が出てきました。radというのは角度の単位の事です。これは弧度法(単位円において、角度を円弧の長さで表す→360°=2πr、180°=π)で表します。まぁ現段階では特に気にしなくても良いでしょう。 ちなみに単位で考えると ωt=[rad/s]×[s]=rad となります。よって、現段階ではradの値だけ考えれば良いです。面倒くさいので公式だけ書きます。ここだけは、質問等は先生か分かる人に聞いて下さい。
ω=2πf[rad/s] (f=周波数[Hz])
・ピーク・ピーク値(peak to peak)
正の最大値から負の最大値までの値。普通、ピーク・ピーク値の半分が最大値である。これについては教科書の図3-4を参考にして下さい。 また、ピーク・ピーク値は電圧を Epp、電流を Ippで表します。
②周期と周波数
サイクルについては詳しくは教科書の図3-4を参照してください。
・周期…1サイクル(1周波)に要する時間。つまりsin0゜地点からsin360゜地点までって事ですね。(記号:T 単位[s])
・周波数…1秒間に何サイクルあるか(何回繰り返しているか)。(記号:f 単位[Hz])
周期Tと周波数fの関係式
f(周波数)=1/T [Hz]
例えば、関東を例にしてみましょう。関東エリアは50Hzの地域だという事は皆さんご存知だと思います。これを上の式に当てはめてみましょう。
f(周波数)=1/T →50=1/T 50T=1 T=1÷50=0,02[s]
という答えが導き出せるはずです。Tとは周期を表す記号なので、周期は0,02[s]です。これを、「マイクロメーター秒」に直してみましょう。1[ms]=0,001[s]なので、0,02[s]=20[ms]となります。
③平均値…半サイクルの平均
なぜ半サイクルなのか…それは、1サイクルの平均は当然0になるからです。(正の最大値と負の最大値の絶対値は等しい) また電圧の平均値をEa、電流の平均値をIaと表します。
交流の平均値と最大値の関係式
Ea(平均値)=(2/π)Em [V]br>
この関係式は正弦波交流の場合にしか通用しません。今のところはそんな事考えなくてOKです。
④実行値…交流の直流換算値?(そういう風に考える)
電圧はV、電流はIを用いて表します。
交流の実行値と最大値の関係式
実行値=(1/√2)×最大値[V]=Em/√2 [V]=Em=√2E
なお、交流の値は、特に断りの無い限り実行値で示す事になっています。 また、位相については試験範囲外なのでカットします。
レポート1
教科書P55.3.実験
(1)正弦波交流電圧の測定
結果はこちらの画像参照。

4.課題
①一般家庭のコンセントの交流電圧は実行値が100[V]である。最大値Em、平均値Ea[V]、およびピーク・ピーク値Epp[V]を求めよ。
答
最大値…Em=100√2=141
ピーク・ピーク値…Epp=282[V]
平均値…Ea=(2/π)141=282/π[V]
br→
main_box